题目内容
已知函数f(x)=
,x∈[1,17].
(1)证明函数f(x)在[1,17]上为增函数;
(2)求此函数的最大值和最小值.
| 2x-1 |
| x+1 |
(1)证明函数f(x)在[1,17]上为增函数;
(2)求此函数的最大值和最小值.
考点:函数单调性的性质,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)利用函数单调性的定义证明即可;
(2)利用(1)的结论,即可求得最值.
(2)利用(1)的结论,即可求得最值.
解答:
(1)证明:设任意的x1,x2∈[1,17],且x1<x2,则
f(x1)-f(x2)=
-
=
,
∵x1,x2∈[1,17],且x1<x2,
∴x1-x2<0,(x1+1)(x2+1)>0,
∴
<0,即f(x1)<f(x2),
∴函数f(x)在[1,17]上为增函数.
(2)解:由(1)可知函数f(x)在[1,17]上为增函数;
∴当x=1时,f(x)有最小值为
;
当x=17时,f(x)有最大值为
.
f(x1)-f(x2)=
| 2x1-1 |
| x1+1 |
| 2x2-1 |
| x2+1 |
| 3(x1-x2) |
| (x1+1)(x2+1) |
∵x1,x2∈[1,17],且x1<x2,
∴x1-x2<0,(x1+1)(x2+1)>0,
∴
| 3(x1-x2) |
| (x1+1)(x2+1) |
∴函数f(x)在[1,17]上为增函数.
(2)解:由(1)可知函数f(x)在[1,17]上为增函数;
∴当x=1时,f(x)有最小值为
| 1 |
| 2 |
当x=17时,f(x)有最大值为
| 11 |
| 6 |
点评:本题主要考查学生对函数的单调性的证明方法---定义法,以及利用函数的单调性求最值的方法,属基础题.

练习册系列答案
相关题目
已知集合A={x|
≥0},集合B={y|y=sinx,x∈R},则B∩CRA=( )
| 1+x |
| 1-x |
| A、∅ | B、{1} |
| C、{-1} | D、{-1,1} |
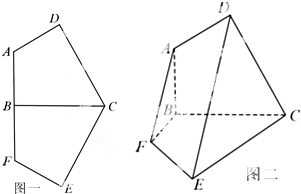 已知轴对称平面五边形ADCEF(如图1),BC为对称轴,AD⊥CD,AD=AB=1,CD=BC=
已知轴对称平面五边形ADCEF(如图1),BC为对称轴,AD⊥CD,AD=AB=1,CD=BC=