题目内容
已知f(x)=
cos2x+2sin(
+x)sin(π-x),x∈R
(Ⅰ)最小正周期及对称轴方程;
(Ⅱ)已知锐角△ABC的内角A,B,C的对边分别为a,b,c,且f(A)=-
,a=3,求BC边上的高的最大值.
| 3 |
| 3π |
| 2 |
(Ⅰ)最小正周期及对称轴方程;
(Ⅱ)已知锐角△ABC的内角A,B,C的对边分别为a,b,c,且f(A)=-
| 3 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的图像与性质,解三角形
分析:(Ⅰ)利用二倍角公式,诱导公式和两角和公式对函数解析式进行化简,利用三角函数图象和性质求得其最小正周期T,及对称轴.
(Ⅱ)利用三角形面积公式得到h和bc的关系式,进而利用余弦定理得到b和c的关系式,利用基本不等式的性质求得bc的最大值,进而求得h的最大值.
(Ⅱ)利用三角形面积公式得到h和bc的关系式,进而利用余弦定理得到b和c的关系式,利用基本不等式的性质求得bc的最大值,进而求得h的最大值.
解答:
解:(Ⅰ)f(x)=
cos2x+2sin(
+x)sin(π-x)=
cos2x-2cosxsinx=
cos2x-sin2x=2(
cos2x-
sin2x)=2cos(2x+
),
∴T=
=π,
令2x+
=kπ(k∈Z),即x=
-
(k∈Z),
∴函数f(x)的对称轴方程为x=
-
(k∈Z),
(Ⅱ)∵f(x)=2cos(2x+
),
∴f(A)=2cos(2A+
)=-
,即cos(2A+
)=-
,
∵0<A<
,
∴
<2A+
<
,
∴2A+
=
,
∴A=
.
设BC边上的高位h,
则S△ABC=
bcsinA=
a•h,即bc=3h,h=
,
∵cosA=
=
=
,
∴bc+9=b2+c2,
∵b2+c2≥2bc,当且仅当b=c时,等号成立.
∴bc+9≥2bc,bc≤9,此时b=c,
∵A=
,
∴b=c=a=3,等号能成立.
∴此时h=
=3.
∴h的最大值为3.
| 3 |
| 3π |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∴T=
| 2π |
| 2 |
令2x+
| π |
| 6 |
| kπ |
| 2 |
| π |
| 12 |
∴函数f(x)的对称轴方程为x=
| kπ |
| 2 |
| π |
| 12 |
(Ⅱ)∵f(x)=2cos(2x+
| π |
| 6 |
∴f(A)=2cos(2A+
| π |
| 6 |
| 3 |
| π |
| 6 |
| ||
| 2 |
∵0<A<
| π |
| 2 |
∴
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴2A+
| π |
| 6 |
| 5π |
| 6 |
∴A=
| π |
| 3 |
设BC边上的高位h,
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| bc |
| 3 |
∵cosA=
| b2+c2-a2 |
| 2bc |
| b2+c2-9 |
| 2bc |
| 1 |
| 2 |
∴bc+9=b2+c2,
∵b2+c2≥2bc,当且仅当b=c时,等号成立.
∴bc+9≥2bc,bc≤9,此时b=c,
∵A=
| π |
| 3 |
∴b=c=a=3,等号能成立.
∴此时h=
| bc |
| 3 |
∴h的最大值为3.
点评:本题主要考查了正弦定理,余弦定理,诱导公式,三角函数恒等变换的应用.考查了基础的知识的综合运用.

练习册系列答案
相关题目
在△ABC中,已知a2tanB=b2tanA,则△ABC该的形状为( )
| A、等腰三角形 |
| B、直角三角形 |
| C、正三角形 |
| D、等腰或直角三角形 |
二项式(2x2-
)6的展开式中第4项的系数是( )
| 1 | |||
|
| A、20 | B、60 |
| C、-160 | D、160 |
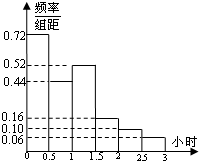 电视传媒为了解某市100万观众对足球节目的收视情况,随机抽取了100名观众进行调查.如图是根据调查结果绘制的观众每周平均收看足球节目时间的频率分布直方图,将每周平均收看足球节目时间不低于1.5小时的观众称为“足球迷”,并将其中每周平均收看足球节目时间不低于2.5小时的观众称为“铁杆足球迷”.
电视传媒为了解某市100万观众对足球节目的收视情况,随机抽取了100名观众进行调查.如图是根据调查结果绘制的观众每周平均收看足球节目时间的频率分布直方图,将每周平均收看足球节目时间不低于1.5小时的观众称为“足球迷”,并将其中每周平均收看足球节目时间不低于2.5小时的观众称为“铁杆足球迷”.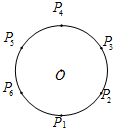 如图,设P1,P2,…,P6为单位圆上逆时针均匀分布的六个点.现从这六个点中任选其中三个不同点构成一个三角形,记该三角形的面积为随机变量S.
如图,设P1,P2,…,P6为单位圆上逆时针均匀分布的六个点.现从这六个点中任选其中三个不同点构成一个三角形,记该三角形的面积为随机变量S.