题目内容
从1,2,3,5中任取2个数字作为直线Ax+By=0中的A、B.
(1)写出这个试验的基本事件空间;
(2)求这条直线的斜率大于-1的概率.
(1)写出这个试验的基本事件空间;
(2)求这条直线的斜率大于-1的概率.
考点:古典概型及其概率计算公式
专题:
分析:(1)从1,2,3,5中任取2个数字作为直线Ax+By=0中的A、B,基本事件总数有
个,利用列举法能求出这个试验的基本事件空间.
(2)这条直线的斜率大于-1包含的基本事件有6个,由此能求出这条直线的斜率大于-1的概率.
| A | 2 4 |
(2)这条直线的斜率大于-1包含的基本事件有6个,由此能求出这条直线的斜率大于-1的概率.
解答:
解:(1)从1,2,3,5中任取2个数字作为直线Ax+By=0中的A、B,
这个试验的基本事件空间为:
Ω={(1,2),(1,3),(1,5),(2,1),(2,3),(2,5),(3,1),(3,2),(3,5),(5,1),(5,2),(5,3)}.
(2)∵直线Ax+By=0的斜率k=-
,
∴这条直线的斜率大于-1包含的基本事件有:
(1,2),(1,3),(1,5),(2,3),(2,5),(3,5),
∴这条直线的斜率大于-1的概率:
p=
=
.
这个试验的基本事件空间为:
Ω={(1,2),(1,3),(1,5),(2,1),(2,3),(2,5),(3,1),(3,2),(3,5),(5,1),(5,2),(5,3)}.
(2)∵直线Ax+By=0的斜率k=-
| A |
| B |
∴这条直线的斜率大于-1包含的基本事件有:
(1,2),(1,3),(1,5),(2,3),(2,5),(3,5),
∴这条直线的斜率大于-1的概率:
p=
| 6 |
| 12 |
| 1 |
| 2 |
点评:本题考查基本事件空间的求法,考查概率的求法,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
下列四个函数中,是奇函数且在区间(-1,0)上为减函数的是( )
A、y=(
| ||
B、y=
| ||
| C、y=log2|x| | ||
| D、y=-x3 |
如图,△AOB是一个水平放置的平面图形的直观图,则其平面图形的面积为( )
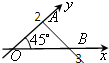

| A、3 | ||||
| B、6 | ||||
C、3
| ||||
D、
|
设|
|=4,|
|=3,夹角为60°,则|
+
|等于( )
| a |
| b |
| a |
| b |
| A、37 | ||
| B、13 | ||
C、
| ||
D、
|
函数y=mx2m-n的导数为y′=4x3,则( )
| A、m=-1,n=-2 |
| B、m=-1,n=2 |
| C、m=1,n=2 |
| D、m=1,n=-2 |
已知圆C:(x-1)2+(y-1)2=4,则C上到l:x+y-4=0的距离为
的点有( )个.
| ||
| 2 |
| A、1 | B、2 | C、3 | D、4 |