题目内容
设|
|=4，|
|=3，夹角为60°，则|
+
|等于（ ）
| a |
| b |
| a |
| b |
| A、37 | ||
| B、13 | ||
C、
| ||
D、
|
考点：平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：根据平面向量的数量积求出向量的模长即可．
解答：
解：∵|
|=4，|
|=3，夹角为60°，
∴(
+
)2=
2+2
•
+
2
=42+2×4×3×cos60°+32
=37；
∴|
+
|=
．
故选：C．
| a |
| b |
∴(
| a |
| b |
| a |
| a |
| b |
| b |
=42+2×4×3×cos60°+32
=37；
∴|
| a |
| b |
| 37 |
故选：C．
点评：本题考查了平面向量的应用问题，解题时应熟记平面向量的数量积的定义与性质，是基础题．
练习册系列答案
相关题目
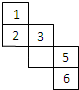正方体的六个面分别用“前面，后面，上面，下面，左面，右面”表示．如图是一个正方体的表面展开图，若图中“4”在正方体的“前面”，则“后面”是（ ）