题目内容
17.已知数列{an}的前n项和Sn=3n2+8n,{bn}是等差数列,且an=bn+bn+1.(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)令cn=bn•2n,求数列{cn}的前n项和Tn.
分析 (Ⅰ)数列{an}的前n项和Sn=3n2+8n,可得a1=11.当n≥2时,an=Sn-Sn-1.可得an.{bn}是等差数列,设公差为d,则an=bn+bn+1=2bn+d.当n=1时,2b1=11-d;当n=2时,2b2=17-d即可得出bn.
(II)cn=bn•2n=(3n+1)•2n.利用错位相减法即可得出.
解答 解:(Ⅰ)∵数列{an}的前n项和Sn=3n2+8n,
∴a1=11.
当n≥2时,an=Sn-Sn-1=3n2+8n-3(n-1)2-8(n-1)=6n+5.
又∵an=6n+5对n=1也成立所以an=6n+5,{bn}是等差数列,设公差为d,则an=bn+bn+1=2bn+d.
当n=1时,2b1=11-d;当n=2时,2b2=17-d
由$\left\{\begin{array}{l}{2{b}_{1}=11-d}\\{2{b}_{2}=17-d}\end{array}\right.$,
解得d=3,b1=4.
所以数列{bn}的通项公式为:bn=4+3(n-1)=3n+1.
(II)cn=bn•2n=(3n+1)•2n.
于是,Tn=4×2+7×22+10×23+…+(3n+1)•2n,
两边同乘以2,得2Tn=4×22+7×23+…+(3n-2)•2n-(3n+1)•2n+1.
两式相减,得-Tn=8+3(22+23+…+2n)-(3n+1)•2n+1=8+3×$\frac{4({2}^{n-1}-1)}{2-1}$-(3n+1)•2n+1.
可得:Tn=4+(3n-2)•2n+1.
点评 本题考查了等差数列与等比数列的通项公式与求和公式、错位相减法、数列递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
7.若f(x)=x4-3x3+1,则f′(x)=( )
| A. | 4x3-6x2 | B. | 4x3-9x2 | C. | 4x3+6x2 | D. | 4x3-6x2+1 |
8.若函数f(x)=$\left\{\begin{array}{l}{1+lo{g}_{2}(3-x),x<1}\\{{2}^{x-1},x≥1}\end{array}\right.$,则f(-1)+f(log26)=( )
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
5.对任意k∈R,直线y=klog2x-2总过一个定点,该定点坐标为( )
| A. | (1,-2) | B. | (-1,2) | C. | (2,-1) | D. | (-2,-1) |
12.y=4cosx-e|x|图象可能是( )
| A. | 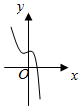 | B. | 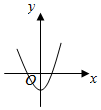 | C. | 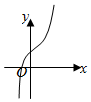 | D. | 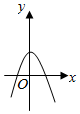 |
7.函数$y=\sqrt{{{log}_{\frac{1}{2}}}({x^2}-2)}$的定义域是( )
| A. | [-$\sqrt{3}$,$\sqrt{3}$] | B. | [-$\sqrt{3}$,-$\sqrt{2}$)∪($\sqrt{2}$,$\sqrt{3}$) | C. | [-3,-1)∪(1,3] | D. | [-$\sqrt{3}$,-$\sqrt{2}$)∪($\sqrt{2}$,$\sqrt{3}$] |