题目内容
12．y=4cosx-e|x|图象可能是（ ）| A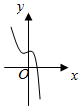． |  | B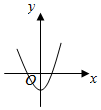． |  | C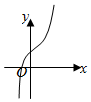． |  | D． |  |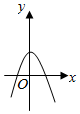
分析 判断函数的奇偶性，计算函数与y轴的交点坐标即可判断出答案．
解答 解：显然y=4cosx-e|x|是偶函数，图象关于y轴对称，排除A，C；
又当x=0时，y=4-1=3＞0，排除B，
故选D．
点评 本题考查了函数图象的判断，一般从奇偶性，单调性，特殊值等方面判断，属于基础题．
练习册系列答案
相关题目
4．
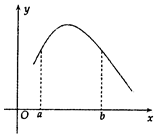函数f（x）的图象如图所示，设f'（x）是f（x）的导函数，若0＜a＜b，下列各式成立的是（ ）
函数f（x）的图象如图所示，设f'（x）是f（x）的导函数，若0＜a＜b，下列各式成立的是（ ）| A． | $f'（{\frac{2ab}{a+b}}）＜f'（{\frac{a+b}{2}}）＜f'（{\sqrt{ab}}）$ | B． | $f'（{\frac{2ab}{a+b}}）＜f'（{\sqrt{ab}}）＜f'（{\frac{a+b}{2}}）$ | ||
| C． | $f'（{\frac{a+b}{2}}）＜f'（{\frac{2ab}{a+b}}）＜f'（{\sqrt{ab}}）$ | D． | $f'（{\frac{a+b}{2}}）＜f'（{\sqrt{ab}}）＜f'（{\frac{2ab}{a+b}}）$ |