题目内容
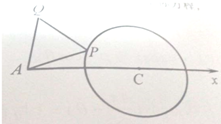 已知半径为2的定圆C外一定点A,且AC=4,在圆上任取一点P,以AP为一边逆时针作等边△APQ,当P在圆上运动时,建立适当的极坐标系,求点Q轨迹的极坐标方程,并转化为直角坐标方程.
已知半径为2的定圆C外一定点A,且AC=4,在圆上任取一点P,以AP为一边逆时针作等边△APQ,当P在圆上运动时,建立适当的极坐标系,求点Q轨迹的极坐标方程,并转化为直角坐标方程.考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:如图所示,以点A为极点,AC为极轴建立极坐标系.设Q(ρ,θ),则|AP|=ρ,∠PAC=θ-60°.在△APC中,利用余弦定理可得:PC2=AP2+AC2-2AP•ACcos(θ-60°),化简即可得出点Q的极坐标方程,再利用
即可得到直角坐标方程.
|
解答:
解:如图所示,以点A为极点,AC为极轴建立极坐标系.
设Q(ρ,θ),则|AP|=ρ,∠PAC=θ-60°.
在△APC中,利用余弦定理可得:PC2=AP2+AC2-2AP•ACcos(θ-60°),
∴22=ρ2+42-2×4ρcos(θ-60°),
化为ρ2-8ρcos(θ-60°)+12=0,即为点Q的极坐标方程.
展开为ρ2-8ρ(
cosθ+
sinθ)+12=0,
∴x2+y2-4x-4
y+12=0即为点Q的直角坐标方程.

设Q(ρ,θ),则|AP|=ρ,∠PAC=θ-60°.
在△APC中,利用余弦定理可得:PC2=AP2+AC2-2AP•ACcos(θ-60°),
∴22=ρ2+42-2×4ρcos(θ-60°),
化为ρ2-8ρcos(θ-60°)+12=0,即为点Q的极坐标方程.
展开为ρ2-8ρ(
| 1 |
| 2 |
| ||
| 2 |
∴x2+y2-4x-4
| 3 |
点评:本题考查了极坐标方程化为直角坐标方程、余弦定理的应用,考查了计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
cos
的值是( )
| 31π |
| 6 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知f(x)=(sinx+cosx)sinx,若f(x1)≤f(x)≤f(x2),对?x∈R成立,则|x1-x2|最小值为( )
A、
| ||
B、
| ||
C、
| ||
| D、π |
已知点F是双曲线
-
=1(a>0,b>0)的右焦点,抛物线y2=4cx(c>0)的准线交该双曲线于A,B两点,若△ABF是锐角三角形且c2=a2+b2,则该双曲线离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,
| ||||
B、(1+
| ||||
C、(
| ||||
D、(1,1+
|