题目内容
设偶函数y=f(x)和奇函数y=g(x)的图象如图所示:集合A={x|f(g(x)-t)=0}与集合B={x|g(f(x)-t)=0}的元素个数分别为a,b,若
<t<1,则b-a的值不可能是( )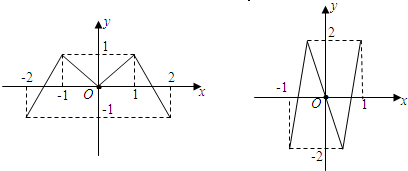
| 1 |
| 2 |
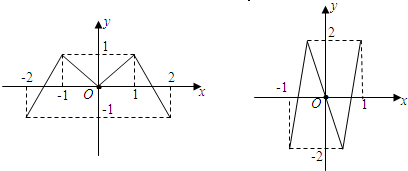
| A、-1 | B、0 | C、1 | D、2 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:利用图象,分别判断g(x)=t和f(x)=t,在
<t<1时的取值情况,然后进行讨论即可.
| 1 |
| 2 |
解答:
解:由条件知,第一个图象为f(x)的图象,第二个为g(x)的图象.
由图象可知若f(x)=0,则x有3个解,为x=--
,x=0,x=
,若g(x)=0,则x有3个解,不妨设为x=n,x=0,x=-n,(0<n<1)
由f(g(x)-t)=0得g(x)-t=
,或g(x)-t=0,或g(x)-t=-
,.
即g(x)=t+
,或g(x)=t,或g(x)=t-
.
当<t<1时,由g(x)=t,得x有3个解.
g(x)=t-
∈(-1,-
),此时x有3个解.
g(x)=t+
∈(2,
),此时方程无解.所以a=3+3=6.
由g(f(x)-t)=0得f(x)-t=n,或f(x)-t=0或f(x)-t=-n.
即f(x)=t+n,或f(x)=t,或f(x)=t-n.
若f(x)=t,因为
<t<1,所以此时x有4个解.
若f(x)=t+n,因为
<t<1,0<n<1,所以若0<n<
,则
<t+n<
,此时x有4个解或2解或0个解.
对应f(x)=t-n∈(0,1)有4个解,此时b=4+4+4=12或b=4+2+4=10或b=4+0+4=8.
若
≤n<1,则1<t+n<2,此时x无解.对应f(x)=t-n∈(-
,
),对应的有2个解或3解或4个解.
所以此时b=4+2=6或b=4+3=7或b=4+4=8.
综上b=12或10或8或6或7.
所以 b-a=6或4或2或0或1.
故A不可能.
故选:A.
由图象可知若f(x)=0,则x有3个解,为x=--
| 3 |
| 2 |
| 3 |
| 2 |
由f(g(x)-t)=0得g(x)-t=
| 3 |
| 2 |
| 3 |
| 2 |
即g(x)=t+
| 3 |
| 2 |
| 3 |
| 2 |
当<t<1时,由g(x)=t,得x有3个解.
g(x)=t-
| 3 |
| 2 |
| 1 |
| 2 |
g(x)=t+
| 3 |
| 2 |
| 5 |
| 2 |
由g(f(x)-t)=0得f(x)-t=n,或f(x)-t=0或f(x)-t=-n.
即f(x)=t+n,或f(x)=t,或f(x)=t-n.
若f(x)=t,因为
| 1 |
| 2 |
若f(x)=t+n,因为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
对应f(x)=t-n∈(0,1)有4个解,此时b=4+4+4=12或b=4+2+4=10或b=4+0+4=8.
若
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以此时b=4+2=6或b=4+3=7或b=4+4=8.
综上b=12或10或8或6或7.
所以 b-a=6或4或2或0或1.
故A不可能.
故选:A.
点评:本题主要考查复合函数的根的取值问题,利用数学结合思想是解决本题的关键,根据参数的不同取值要进行分类讨论,综合性较强,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
数列3,5,9,17,33…的一个通项公式是( )
| A、an=2n |
| B、an=2n+1 |
| C、an=3n |
| D、an=2n-1 |
函数y=x+
(x>0)的值域为( )
| 1 |
| x |
| A、(-∞,-2]∪[2,+∞) |
| B、(0,+∞) |
| C、[2,+∞) |
| D、(2,+∞) |
已知函数f(x)=xlnx,若直线l过点(0,-1),并且与曲线y=f(x)相切,则直线l的方程为( )
| A、x+y-1=0 |
| B、x-y-1=0 |
| C、x+y+1=0 |
| D、x-y+1=0 |
比较sin
,sin
,sin
的大小关系是( )
| π |
| 6 |
| π |
| 8 |
| 3π |
| 8 |
A、sin
| ||||||
B、sin
| ||||||
C、sin
| ||||||
D、sin
|
下列说法正确的是( )
| A、方向相同或相反的向量是平行向量 | ||
B、零向量是
| ||
| C、长度相等的向量叫做相等向量 | ||
| D、共线向量是在一条直线上的向量 |
若实数x,y满足约束条件
,则z=x-y的最大值是( )
|
| A、-1 | B、0 | C、1 | D、2 |
| ∫ | 2 -2 |
| A、0 | B、1 | C、8 | D、16 |