题目内容
| ∫ | 2 -2 |
| A、0 | B、1 | C、8 | D、16 |
考点:定积分
专题:导数的概念及应用
分析:根据定积分的计算公式计算即可.
解答:
解:
x3dx=
x4
=0.
故选:A
| ∫ | 2 -2 |
| 1 |
| 4 |
| | | 2 -2 |
故选:A
点评:本题考查了积分运算,解答的关键是正确找出被积函数的原函数.

练习册系列答案
相关题目
设偶函数y=f(x)和奇函数y=g(x)的图象如图所示:集合A={x|f(g(x)-t)=0}与集合B={x|g(f(x)-t)=0}的元素个数分别为a,b,若
<t<1,则b-a的值不可能是( )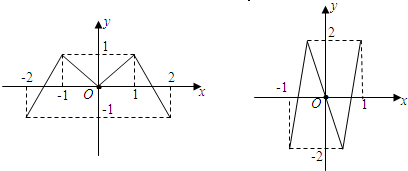
| 1 |
| 2 |
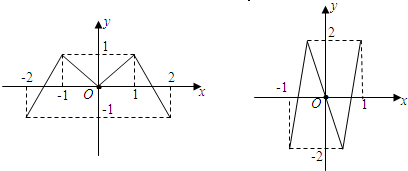
| A、-1 | B、0 | C、1 | D、2 |
图示是由几个相同的小正方体搭成的一个几何体,它的俯视图是( )


A、 |
B、 |
C、 |
D、 |
圆上有10个点,过每三个点画一个圆内接三角形,则一共可以画的三角形个数为( )
| A、720 | B、360 |
| C、240 | D、120 |
已知等差数列{an},满足a3+a8=6,则此数列的前10项的和S10=( )
| A、10 | B、20 | C、30 | D、60 |
| ∫ | a 0 |
| A、2 | B、-1 | C、0 | D、1 |
已知函数f(x)是奇函数,且当x>0时,f(x)=x2+
,则f(-1)=( )
| 1 |
| x |
| A、-2 | B、0 | C、1 | D、2 |
已知数列{an}满足a1=1,an+1=
an,n∈N*,其前n项和为Sn,则( )
| 2 |
| 3 |
| A、Sn=2an-1 |
| B、Sn=3an-2 |
| C、Sn=4-3an |
| D、Sn=3-2an |