题目内容
下列说法正确的是（ ）
| A、方向相同或相反的向量是平行向量 | ||
B、零向量是
| ||
| C、长度相等的向量叫做相等向量 | ||
| D、共线向量是在一条直线上的向量 |
考点：平行向量与共线向量
专题：计算题,平面向量及应用
分析：利用平面向量的基本概念逐项检验即可得到答案．
解答：
解：方向相同或相反的非零是平行向量，故排除A；
零向量是既有大小，又有方向的量，故B正确；
长度相等且方向相同的向量叫相等向量，排除C；
共线向量可以在一条直线上，但所在直线也可平行，排除D．
故选B．
零向量是既有大小，又有方向的量，故B正确；
长度相等且方向相同的向量叫相等向量，排除C；
共线向量可以在一条直线上，但所在直线也可平行，排除D．
故选B．
点评：该题考查平行向量、相等向量、零向量等概念，属基础题，正确理解有关概念是解题关键．
练习册系列答案
全能测控一本好卷系列答案
发散思维新课堂系列答案
相关题目
| a |
| b |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设偶函数y=f（x）和奇函数y=g（x）的图象如图所示：集合A={x|f（g（x）-t）=0}与集合B={x|g（f（x）-t）=0}的元素个数分别为a，b，若
＜t＜1，则b-a的值不可能是（ ）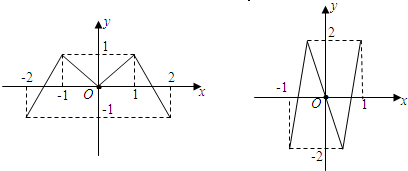
| 1 |
| 2 |
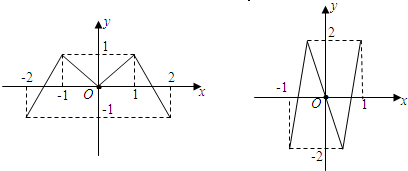
| A、-1 | B、0 | C、1 | D、2 |
若复数z满足z=
，则z的虚部为（ ）
| 5 |
| 3-4i |
| A、-4 | ||
B、-
| ||
| C、4 | ||
D、
|
在等差数列{an}中，a1=2，a8=30，则前8项之和S8=（ ）
| A、128 | B、120 |
| C、124 | D、118 |
抛一枚均匀硬币，正反每面出现的概率都是
，反复这样投掷，数列{an}定义如下：an=
，若Sn=a1+a2+…+an（n∈N*），则事件“S2≠0，S8=2”的概率是（ ）
| 1 |
| 2 |
|
A、
| ||
B、
| ||
C、
| ||
D、
|
图示是由几个相同的小正方体搭成的一个几何体，它的俯视图是（ ）
A、 |
B、 |
C、 |
D、 |
已知函数f（x）是奇函数，且当x＞0时，f（x）=x2+
，则f（-1）=（ ）
| 1 |
| x |
| A、-2 | B、0 | C、1 | D、2 |