题目内容
函数y=x+
（x＞0）的值域为（ ）
| 1 |
| x |
| A、（-∞，-2]∪[2，+∞） |
| B、（0，+∞） |
| C、[2，+∞） |
| D、（2，+∞） |
考点：基本不等式
专题：计算题,不等式的解法及应用
分析：利用基本不等式可求函数的最小值，由此可得函数值域．
解答：
解：∵x＞0，
∴x+
≥2
=2，当且仅当x=
即x=1时取等号，
∴函数y=x+
（x＞0）的值域为[2，+∞），
故选：C．
∴x+
| 1 |
| x |
x•
|
| 1 |
| x |
∴函数y=x+
| 1 |
| x |
故选：C．
点评：该题考查利用基本不等式求函数的最值，属基础题，熟记基本不等式求最值的条件是解题关键．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
设a=
sinxdx，二项式（
+
）5的展开式中的第三项为M，第四项为N，则M+N的最小值为（ ）
| ∫ | π 0 |
| |x| |
| a |
| 1 |
| |x| |
A、5
| ||||
B、
| ||||
C、
| ||||
D、2
|
| a |
| b |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
将甲，乙两名同学5次物理测验的成绩用茎叶图表示如图，若甲，乙两人成绩的中位数分别是x甲，x乙，下列说法正确的是（ ）| A、x甲＜x乙，乙比甲成绩稳定 |
| B、x甲＞x乙；甲比乙成绩稳定 |
| C、x甲＞x乙；乙比甲成绩稳定 |
| D、x甲＜x乙；甲比乙成绩稳定 |
设偶函数y=f（x）和奇函数y=g（x）的图象如图所示：集合A={x|f（g（x）-t）=0}与集合B={x|g（f（x）-t）=0}的元素个数分别为a，b，若
＜t＜1，则b-a的值不可能是（ ）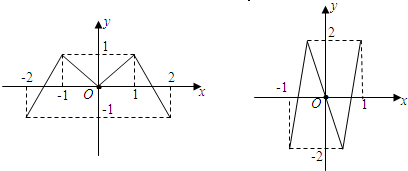
| 1 |
| 2 |
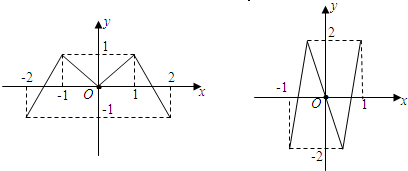
| A、-1 | B、0 | C、1 | D、2 |
在等差数列{an}中，a1=2，a8=30，则前8项之和S8=（ ）
| A、128 | B、120 |
| C、124 | D、118 |
圆上有10个点，过每三个点画一个圆内接三角形，则一共可以画的三角形个数为（ ）
| A、720 | B、360 |
| C、240 | D、120 |