题目内容
袋子里装有大小相同的黑白两色的手套,黑色手套15支,白色手套10只,现从中随机地取出2只手套,如果2只是同色手套则甲获胜,2只手套颜色不同则乙获胜.试问:甲、乙获胜的机会是( )
| A、甲多 | B、乙多 |
| C、一样多 | D、不确定 |
考点:极差、方差与标准差
专题:概率与统计
分析:求出从25只中随机地取出2只手套的取法有多少种,其中2只是同色手套的取法是多少种,颜色不同的取法有多少种;即可计算甲、乙获胜的概率.
解答:
解:从25只中随机地取出2只手套,共有
种取法,
其中2只是同色手套的取法,共有
+
=105+45=150种;
2只手套颜色不同的取法,共有
×
=15×10=150种;
甲获胜的概率是P1=
,乙获胜的概率是P2=
;
∴甲、乙获胜的机会一样多.
故选:C..
| C | 2 25 |
其中2只是同色手套的取法,共有
| C | 2 15 |
| C | 2 10 |
2只手套颜色不同的取法,共有
| C | 1 15 |
| C | 1 10 |
甲获胜的概率是P1=
| 150 | ||
|
| 150 | ||
|
∴甲、乙获胜的机会一样多.
故选:C..
点评:本题考查了古典概率的应用问题,解题时应用分步相乘原理与分类相加原理进行计算,是基础题.

练习册系列答案
相关题目
已知函数y=f(x)是定义域为R的偶函数.当x≥0时,f(x)=
若关于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且仅有6个不同实数根,则实数a的取值范围是( )
|
A、(-
| ||||||
B、(-
| ||||||
C、(-
| ||||||
D、(-
|
若集合M={y|y=2-x},N={x|y=
},则M∩N等于( )
| x-1 |
| A、{y|y>1} |
| B、{y|y≥1} |
| C、{y|y>0} |
| D、{y|y≥0} |
| ∫ | 2 1 |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x3 |
A、ln2+
| ||
B、ln2-
| ||
C、ln2-
| ||
D、ln2-
|
已知log2m=2.013,log2n=1.013,则
等于( )
| n |
| m |
| A、2 | ||
B、
| ||
| C、10 | ||
D、
|
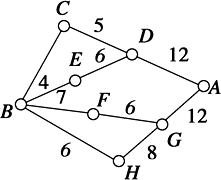 如图所示,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,已知单位时间内传递的最大信息量为19,则从结点C向结点B单位时间内可以通过的最大信息量为
如图所示,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,已知单位时间内传递的最大信息量为19,则从结点C向结点B单位时间内可以通过的最大信息量为