题目内容
11.已知函数f(x)=2sinx+tanx-2x.(1)证明:函数f(x)在$(-\frac{π}{2},\frac{π}{2})$上单调递增;
(2)若$x∈(0,\frac{π}{2})$,f(x)<mx2,求m的取值范围.
分析 (1)求出函数的导数,得到导函数是非负数,求出函数的单调性即可;
(2)通过讨论m的范围,结合函数的单调性求出m的具体范围即可.
解答 解:(1)证明:$f'(x)=cosx+\frac{1}{{{{cos}^2}x}}-2$,
因为$x∈(-\frac{π}{2},\frac{π}{2})$,所以cosx∈(0,1],
于是$f'(x)=2cosx+\frac{1}{{{{cos}^2}x}}-2≥{cos^2}x+\frac{1}{{{{cos}^2}x}}-2≥0$(等号当且仅当x=0时成立).
故函数f(x)在$(-\frac{π}{2},\frac{π}{2})$上单调递增.
(2)由(1)得f(x)在$(0,\frac{π}{2})$上单调递增,
又f(0)=0,所以f(x)>0,
(ⅰ)当m≤0时,f(x)>0≥mx2成立.
(ⅱ)当m>0时,令p(x)=sinx-x,则p'(x)=cosx-1,
当$x∈(0,\frac{π}{2})$时,p'(x)<0,p(x)单调递减,
又p(0)=0,所以p(x)<0,
故$x∈(0,\frac{π}{2})$时,sinx<x.(*)
由(*)式可得f(x)-mx2=sinx+tanx-2x-mx2<tanx-x-mx2,
令g(x)=tanx-x-mx2,则g'(x)=tan2x-2mx
由(*)式可得$g'(x)<\frac{x^2}{{{{cos}^2}x}}-2mx=\frac{x}{{{{cos}^2}x}}(x-2m{cos^2}x)$
令h(x)=x-2mcos2x,得h(x)在$(0,\frac{π}{2})$上单调递增,
又h(0)<0,$h(\frac{π}{2})>0$,所以存在$t∈(0,\frac{π}{2})$使得h(t)=0,
即x∈(0,t)时,h(x)<0,
所以x∈(0,t)时,g'(x)<0,g(x)单调递减,
又g(0)=0,所以g(x)<0,
即x∈(0,t)时,f(x)-mx2<0,与f(x)>mx2矛盾.
综上,满足条件的m的取值范围是(-∞,0].
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道综合题.

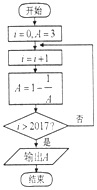 阅读如图的程序框图,运行相应的程序,输出的结果为( )
阅读如图的程序框图,运行相应的程序,输出的结果为( )| A. | 3 | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
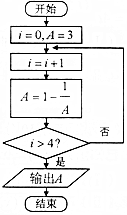 阅读如图的程序框图,运行相应的程序,输出的结果为( )
阅读如图的程序框图,运行相应的程序,输出的结果为( )| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 3 |
| A. | e0=1与ln 1=0 | B. | log39=2与9${\;}^{\frac{1}{2}}$=3 | ||
| C. | 8${\;}^{-\frac{1}{3}}$=$\frac{1}{2}$与log8$\frac{1}{2}$=-$\frac{1}{3}$ | D. | log77=1与71=7 |