题目内容
19．已知函数f（x）=|x+2|-|x-2|+m（m∈R）．（Ⅰ）若m=1，求不等式f（x）≥0的解集；
（Ⅱ）若方程f（x）=x有三个实根，求实数m的取值范围．
分析 （Ⅰ）分x≤-2，-2＜x＜2，x≥2三种情况求解；
（Ⅱ）由方程f（x）=x可变形为m=x+|x-2|-|x+2|．令$h（x）=x+|x-2|-|x+2|=\left\{\begin{array}{l}x+4，x＜-2\\-x，-2≤x≤2\\ x-4，x＞2.\end{array}\right.$作出图象如图所示．根据图象求解．
解答 解：（Ⅰ）∵m=1时，f（x）=|x+2|-|x-2|+1．
∴当x≤-2时，f（x）=-3，不可能非负；
当-2＜x＜2时，f（x）=2x+1，由f（x）≥0可解得$x≥-\frac{1}{2}$，于是$-\frac{1}{2}≤x＜2$；
当x≥2时，f（x）=5＞0恒成立．
所以不等式f（x）≥0的解集为$[-\frac{1}{2}，+∞）$．
（Ⅱ）由方程f（x）=x可变形为m=x+|x-2|-|x+2|．
令$h（x）=x+|x-2|-|x+2|=\left\{\begin{array}{l}x+4，x＜-2\\-x，-2≤x≤2\\ x-4，x＞2.\end{array}\right.$
作出图象如图所示．
于是由题意可得-2＜m＜2．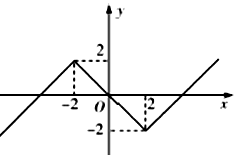
点评 本题考查了绝对值不等式的解法，函数与方程的思想，属于中档题．
练习册系列答案
相关题目
4．
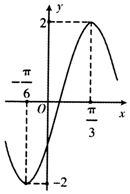函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，-π＜φ＜0）的部分图象如图所示，为了得到g（x）=Asinωx的图象，只需将函数y=f（x）的图象（ ）
函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，-π＜φ＜0）的部分图象如图所示，为了得到g（x）=Asinωx的图象，只需将函数y=f（x）的图象（ ）| A． | 向左平移$\frac{π}{6}$个单位长度 | B． | 向左平移$\frac{π}{12}$个单位长度 | ||
| C． | 向右平移$\frac{π}{6}$个单位长度 | D． | 向右平移$\frac{π}{12}$个单位长度 |
2．已知数列{an}满足an=$\left\{\begin{array}{l}{（\frac{1}{2}-a）n+1（n＜6）}\\{{a}^{n-5}（n≥6）}\end{array}\right.$若对于任意的n∈N*都有an＞an+1，则实数a的取值范围是（ ）
| A． | （0，$\frac{1}{2}$） | B． | （$\frac{1}{2}$，$\frac{7}{12}$） | C． | （$\frac{1}{2}$，1） | D． | （$\frac{7}{12}$，1） |