题目内容
20.若${C}_{n}^{0}$+${C}_{n}^{1}$+…+${C}_{n}^{n}$=256,则${(x+\frac{1}{2\sqrt{x}})}^{n}$的展开式中含x5项的系数为7.(用数字作答)分析 根据组合数公式求出n的值,再利用二项式展开式的通项公式求出展开式中含x5项的系数.
解答 解:${C}_{n}^{0}$+${C}_{n}^{1}$+…+${C}_{n}^{n}$=2n=256,
∴n=8;
∴${(x+\frac{1}{2\sqrt{x}})}^{8}$展开式中,通项公式为:
Tr+1=${C}_{8}^{r}$•x8-r•${(\frac{1}{2\sqrt{x}})}^{r}$=${(\frac{1}{2})}^{r}$•${C}_{8}^{r}$•${x}^{8-\frac{3}{2}r}$,
令8-$\frac{3}{2}$r=5,解得r=2;
∴展开式中含x5项的系数为${(\frac{1}{2})}^{2}$•${C}_{8}^{2}$=7.
故答案为:7.
点评 本题考查了组合数公式与二项式定理的应用问题,是基础题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
15.在国际风帆比赛中,成绩以低分为优胜,比赛共11场,并以最佳的9场成绩计算最终的名次.在一次国际风帆比赛中,前7场比赛结束后,排名前8位的选手积分如表:
(1)根据表中的比赛数据,比较A与B的成绩及稳定情况;
(2)从前7场平均分低于6.5的运动员中,随机抽取2个运动员进行兴奋剂检查,求至少1个运动员平均分不低于5分的概率.
(3)请依据前7场比赛的数据,预测冠亚军选手,并说明理由.
| 运动员 | 比赛场次 | 总分 | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ||
| A | 3 | 2 | 2 | 2 | 4 | 2 | 6 | 21 | ||||
| B | 1 | 3 | 5 | 1 | 10 | 4 | 4 | 28 | ||||
| C | 9 | 8 | 6 | 1 | 1 | 1 | 2 | 28 | ||||
| D | 7 | 8 | 4 | 4 | 3 | 1 | 8 | 35 | ||||
| E | 3 | 12 | 5 | 8 | 2 | 7 | 5 | 42 | ||||
| F | 4 | 11 | 6 | 9 | 3 | 6 | 8 | 47 | ||||
| G | 10 | 12 | 12 | 8 | 12 | 10 | 7 | 71 | ||||
| H | 12 | 12 | 6 | 12 | 7 | 12 | 12 | 73 | ||||
(2)从前7场平均分低于6.5的运动员中,随机抽取2个运动员进行兴奋剂检查,求至少1个运动员平均分不低于5分的概率.
(3)请依据前7场比赛的数据,预测冠亚军选手,并说明理由.
2.已知数列{an}满足an=$\left\{\begin{array}{l}{(\frac{1}{2}-a)n+1(n<6)}\\{{a}^{n-5}(n≥6)}\end{array}\right.$若对于任意的n∈N*都有an>an+1,则实数a的取值范围是( )
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,$\frac{7}{12}$) | C. | ($\frac{1}{2}$,1) | D. | ($\frac{7}{12}$,1) |
3.函数$y=\frac{{|{x+1}|-|{x-1}|}}{{\sqrt{x^2}+1}}$是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
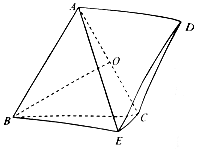 在多面体ABCDE中,平面ABC⊥平面BCE,四边形ABED为平行四边形,AB=AC=BC=2,CE=1,BE=$\sqrt{5}$,O为AC的中点.
在多面体ABCDE中,平面ABC⊥平面BCE,四边形ABED为平行四边形,AB=AC=BC=2,CE=1,BE=$\sqrt{5}$,O为AC的中点.