题目内容
16.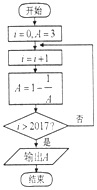 阅读如图的程序框图,运行相应的程序,输出的结果为( )
阅读如图的程序框图,运行相应的程序,输出的结果为( )| A. | 3 | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
分析 模拟程序框图运行过程,总结规律,A的取值周期为3,由于2017=666×3+1,可得当i=2018时满足条件i>2017,退出循环,输出A的值为-$\frac{1}{2}$.
解答 解:模拟程序的运行,可得
i=0,A=3,
执行循环体,i=1,A=$\frac{2}{3}$,
不满足条件i>2017,执行循环体,i=2,A=-$\frac{1}{2}$
不满足条件i>2017,执行循环体,i=3,A=3
不满足条件i>2017,执行循环体,i=4,A=$\frac{2}{3}$
…
观察规律可得A的取值周期为3,由于2017=666×3+1,可得:
不满足条件i>2017,执行循环体,i=2017,A=$\frac{2}{3}$
不满足条件i>2017,执行循环体,i=2018,A=-$\frac{1}{2}$
满足条件i>2017,退出循环,输出A的值为-$\frac{1}{2}$.
故选:D.
点评 本题考查了求程序框图运行结果的问题,解题时应模拟程序框图运行过程,总结规律,得出结论,属于基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
6.若集合$A=({0,\left.{\frac{1}{4}}]}\right.$,则∁RA=( )
| A. | ($\frac{1}{4}$,+∞) | B. | (-∞,0]∪($\frac{1}{4}$,+∞) | C. | (-∞,0]∪[$\frac{1}{4}$,+∞) | D. | [$\frac{1}{4}$,+∞) |
4.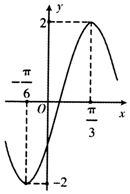 函数f(x)=Acos(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图所示,为了得到g(x)=Asinωx的图象,只需将函数y=f(x)的图象( )
函数f(x)=Acos(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图所示,为了得到g(x)=Asinωx的图象,只需将函数y=f(x)的图象( )
 函数f(x)=Acos(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图所示,为了得到g(x)=Asinωx的图象,只需将函数y=f(x)的图象( )
函数f(x)=Acos(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图所示,为了得到g(x)=Asinωx的图象,只需将函数y=f(x)的图象( )| A. | 向左平移$\frac{π}{6}$个单位长度 | B. | 向左平移$\frac{π}{12}$个单位长度 | ||
| C. | 向右平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{12}$个单位长度 |
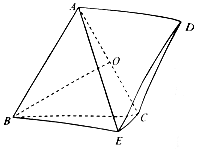 在多面体ABCDE中,平面ABC⊥平面BCE,四边形ABED为平行四边形,AB=AC=BC=2,CE=1,BE=$\sqrt{5}$,O为AC的中点.
在多面体ABCDE中,平面ABC⊥平面BCE,四边形ABED为平行四边形,AB=AC=BC=2,CE=1,BE=$\sqrt{5}$,O为AC的中点.