题目内容
16．已知点O为△ABC外接圆的圆心，且$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\vec 0$，则△ABC的内角A等于（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
分析 由已知向量等式可得O为三角形ABC的重心，结合O又是三角形外接圆的圆心，可得三角形ABC为正三角形，则角A可求．
解答 解：由$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\vec 0$，得$\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OC}$，可知，O为△ABC的重心，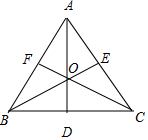
延长AO交BC于D，则D为BC的中点，
又O为△ABC外接圆的圆心，可得AD⊥BC，则AB=AC，
同理可得AB=BC，则△ABC为正三角形，
∴∠A=60°．
故选：C．
点评 本题考查向量加减混合运算及其几何意义，考查三角形重心及外接圆的圆心的性质，是中档题．
练习册系列答案
相关题目
6．函数f（x）=（x3-3x）sinx的大致图象是（ ）
| A． |  | B． |  | C． |  | D． |  |
7．已知a，b∈R，i为虚数单位，且a-3i=2+bi，则复数z=a+bi在复平面上对应的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
4．已知两组数A：x1，x2，x3，x4，x5，x6，x7，B：y1，y2，y3，y4，y5，y6，y7，其中yi=2xi+3，（i=1，2，3，4，5，6，7），A组数的平均数与方差分别记为$\overline{x}$，SA2，B组数的平均数与方差分别记为$\overline{y}$，SB2，则下面关系式正确的是（ ）
| A． | $\overline{y}$=2$\overline{x}$+3，sB2=2sB2+3 | B． | $\overline{y}$=2$\overline{x}$+3，sB2=4sA2 | ||
| C． | $\overline{y}$=2$\overline{x}$，sB2=4sA2 | D． | $\overline{y}$=2$\overline{x}$，sB2=4sA2+3 |
11．过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点F作倾斜角为α的直线交椭圆x轴上方于一点P，其中α∈[$\frac{2π}{3}$，$\frac{5π}{6}$]，$\overrightarrow{OQ}$=$\frac{1}{2}$（$\overrightarrow{OP}$+$\overrightarrow{OF}$），|$\overrightarrow{OQ}$|=$\sqrt{{a}^{2}-{b}^{2}}$，则椭圆离心率的最大值为（ ）
| A． | $\frac{\sqrt{3}-1}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | 1-$\frac{\sqrt{2}}{2}$ |
8．抛掷一颗骰子两次，在第一次掷得向上一面点数是偶数的条件下，则第二次掷得向上一面点数也是偶数的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{4}{7}$ | D． | $\frac{4}{5}$ |