题目内容
直线l：y-1=k（x+2）必经过定点 ．
考点：恒过定点的直线
专题：直线与圆
分析：化直线的方程为y-1=k[x-（-2）]，由直线的点斜式方程可得．
解答：
解：∵直线l的方程为：y-1=k（x+2），
即y-1=k[x-（-2）]，
由直线的点斜式方程可知直线过定点（-2，1）
故答案为：（-2，1）
即y-1=k[x-（-2）]，
由直线的点斜式方程可知直线过定点（-2，1）
故答案为：（-2，1）
点评：本题考查直线恒过定点问题，利用点斜式方程是解决问题的关键，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
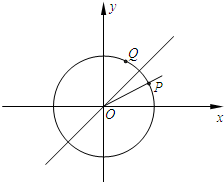如图，已知单位圆上两点P，Q关于直线y=x对称，且以x轴正半轴为始边、以射线OP为终边的角的大小为x．
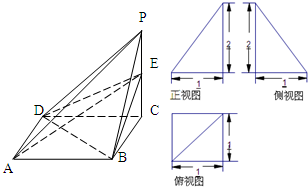已知四棱锥P-ABCD的三视图和直观图如图所示，其中正视图、侧视图是直角三角形，俯视图是有一条对角线的正方形．E是侧棱PC上的动点．
某市高二数学期中考试中，对90分及其以上的成绩情况进行统计，其频率分布直方图如图所示，若（130，140]分数段的人数为10人，则（90，100]分数段的人数为