题目内容
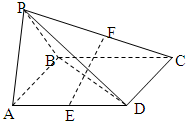 如图,四棱锥P-ABCD的底面是平行四边形,∠BAD=60°,平面PAB⊥平面ABCD,PA=PB=AB=
如图,四棱锥P-ABCD的底面是平行四边形,∠BAD=60°,平面PAB⊥平面ABCD,PA=PB=AB=| 1 |
| 2 |
(Ⅰ)求证:BD⊥平面PAB
(Ⅱ)求证:EF⊥平面PBD
(Ⅲ)若AB=2,求直线AD与平面PBD所成的角的正弦值.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)证明BD⊥AB,利用平面PAB⊥平面ABCD,可得BD⊥平面PAB;
(Ⅱ)设点G是PB的中点,连结AG,FG,证明AG∥EF,AG⊥平面PBD,即可证明EF⊥面PBD;
(Ⅲ)∠ADG就是直线AD与平面PBD所成的角,求出AG,AD,即可求直线AD与平面PBD所成的角的正弦值.
(Ⅱ)设点G是PB的中点,连结AG,FG,证明AG∥EF,AG⊥平面PBD,即可证明EF⊥面PBD;
(Ⅲ)∠ADG就是直线AD与平面PBD所成的角,求出AG,AD,即可求直线AD与平面PBD所成的角的正弦值.
解答:
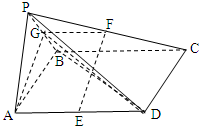 (I)证明:设PA=PB=AB=
(I)证明:设PA=PB=AB=
AD=1,则
BD2=AB2+AD2-2AB•AD•cos60°=3,
故BD2+AB2=AD2,∴BD⊥AB
而平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,
∴BD⊥平面PAB; …(4分)
(II)证明:设点G是PB的中点,连结AG,FG,
则FG∥BC∥AE,FG=
BC=AE
∴四边形AEFG是平行四边形
故AG∥EF …(6分)
∵BD⊥平面PAB,∴平面PBD⊥平面PAB,
在正三角形PAB中,AG⊥PB,故AG⊥平面PBD,…(7分)
而AG∥EF,∴EF⊥平面PBD …(8分)
(Ⅲ)解:连结GD,由( II)知:AG⊥平面PBD,
故∠ADG就是直线AD与平面PBD所成的角 …(10分)
∵AB=2,AD=4,在正三角形PAB中,AG=
,
∴sin∠ADG=
=
,故所求角的正弦值为
…(12分)
 (I)证明:设PA=PB=AB=
(I)证明:设PA=PB=AB=| 1 |
| 2 |
BD2=AB2+AD2-2AB•AD•cos60°=3,
故BD2+AB2=AD2,∴BD⊥AB
而平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,
∴BD⊥平面PAB; …(4分)
(II)证明:设点G是PB的中点,连结AG,FG,
则FG∥BC∥AE,FG=
| 1 |
| 2 |
∴四边形AEFG是平行四边形
故AG∥EF …(6分)
∵BD⊥平面PAB,∴平面PBD⊥平面PAB,
在正三角形PAB中,AG⊥PB,故AG⊥平面PBD,…(7分)
而AG∥EF,∴EF⊥平面PBD …(8分)
(Ⅲ)解:连结GD,由( II)知:AG⊥平面PBD,
故∠ADG就是直线AD与平面PBD所成的角 …(10分)
∵AB=2,AD=4,在正三角形PAB中,AG=
| 3 |
∴sin∠ADG=
| AG |
| AD |
| ||
| 4 |
| ||
| 4 |
点评:本题考查空间几何体中直线与平面平行的判定定理以及直线与平面垂直的判定定理的应用,直线与平面所成角的求法,考查逻辑推理能力与计算能力.

练习册系列答案
相关题目