题目内容
 如图,向量
如图,向量| OZ |
| 4 |
| z |
| A、1+3i | B、-3+i |
| C、3-i | D、3+i |
考点:复数的代数表示法及其几何意义
专题:数系的扩充和复数
分析:利用复数与向量的对应关系可得z=1-i,再利用复数的运算法则即可得出.
解答:
解:∵向量
对应的复数为z,∴z=1-i.
∴z+
=1-i+
=1-i+
=1-i+2(1+i)=3+i.
∴z+
对应的复数为:3+i.
故选:D.
| OZ |
∴z+
| 4 |
| z |
| 4 |
| 1-i |
| 4(1+i) |
| (1-i)(1+i) |
∴z+
| 4 |
| z |
故选:D.
点评:本题考查了复数与向量的对应关系、复数的运算法则,属于基础题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 一个简单组合体的三视图及尺寸如图所示(单位:cm),该组合体的体积为( )
一个简单组合体的三视图及尺寸如图所示(单位:cm),该组合体的体积为( )| A、42cm3 |
| B、48cm3 |
| C、56cm3 |
| D、44cm3 |
在某次测量中得到的A样本数据如下:42,43,46,52,42,50,若B样本数据恰好是A样本数据每个都减5后所得数据,则A、B两样本的下列数字特征对应相同的是( )
| A、平均数 | B、标准差 |
| C、众数 | D、中位数 |
设变量x,y满足约束条件
,则目标函数z=3x-y的最小值为( )
|
| A、-8 | B、-6 | C、-4 | D、-2 |
关于x的不等式ax-b>0的解集为(-∞,1),则不等式
>0的解集为( )
| x-2 |
| ax-b |
| A、(-1,2) |
| B、(-∞,1)∪(1,2) |
| C、(1,2) |
| D、(-∞,-1)∪(-1,2) |
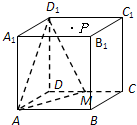 如图,正方体ABCD-A1B1C1D1的棱长为2,P是底面A1B1C1D1的中心,M是CD的中点,则P到平面AMD1的距离为
如图,正方体ABCD-A1B1C1D1的棱长为2,P是底面A1B1C1D1的中心,M是CD的中点,则P到平面AMD1的距离为