题目内容
10．4位同学各自在阳光体育时间活动，可以选择足球和篮球两项运动中一项，则这两项活动都有同学选择的概率为（ ）| A． | $\frac{1}{8}$ | B． | $\frac{3}{8}$ | C． | $\frac{5}{8}$ | D． | $\frac{7}{8}$ |
分析 先求出基本事件总数，由此利用对立事件概率计算公式能求出这两项活动都有同学选择的概率．
解答 解：4位同学各自在阳光体育时间活动，可以选择足球和篮球两项运动中一项，
基本事件总数n=24=16，
这两项活动都有同学选择的概率为：
p=1-$\frac{{1}_{\;}^{\;}}{{2}^{4}}$-$\frac{1}{{2}^{4}}$=$\frac{7}{8}$．
故选：D．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意对立事件概率计算公式的合理运用．
练习册系列答案
相关题目
1．已知点F1，F2为椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左右焦点，若椭圆上存在点P使得$|{\overrightarrow{P{F_1}}}|=2|{\overrightarrow{P{F_2}}}|$，则此椭圆的离心率的取值范围是（ ）
| A． | （0，$\frac{1}{3}$） | B． | （0，$\frac{1}{2}$] | C． | （$\frac{1}{3}$，$\frac{1}{2}$] | D． | [$\frac{1}{3}$，1） |
在△ABC中．
5．变量x，y满足约束条件$\left\{\begin{array}{l}x+y-2≥0\\ x-y-2≤0\\ y≥1\end{array}\right.$，则目标函数z=x+3y的最小值为（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
15．某班有男、女优秀少先队员各2名，现需选出2名优秀少先队员到社区做公益宣传活动，则选出的两名队员性别相同的概率为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
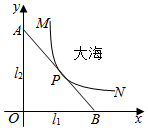某沿海城市的海边有两条相互垂直的直线型公路l1、l2，海岸边界MPN近似地看成一条曲线段．为开发旅游资源，需修建一条连接两条公路的直线型观光大道AB，且直线AB与曲线MPN有且仅有一个公共点P（即直线与曲线相切），如图所示．若曲线段MPN是函数$y=\frac{a}{x}$图象的一段，点M到l1、l2的距离分别为8千米和1千米，点N到l2的距离为10千米，点P到l2的距离为2千米．以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy．