题目内容
20.已知圆O1:(x-2)2+y2=16和圆O2:x2+y2=r2(0<r<2),动圆M与圆O1、圆O2都相切,切圆圆心M的轨迹为两个椭圆,这两个椭圆的离心率分别为e1,e2(e1>e2),则e1+2e2的最小值是$\frac{3+2\sqrt{2}}{4}$.分析 讨论:①当动圆M与圆O1、O2都相内切时,②当动圆M与圆O1相内切而与O2相外切时,分别求出e1、e2(e1>e2),利用基本不等式求出e1+2e2的最小值.
解答 解:①当动圆M与圆O1、O2都相内切时,
|MO2|+|MO1|=4-r=2a,
∴e1=$\frac{2}{4-r}$.
②当动圆M与圆O1相内切而与O2相外切时,
|MO1|+|MO2|=4+r=2a′,
∴e2=$\frac{2}{4+r}$,
∴e1+2e2=$\frac{2}{4-r}$+$\frac{4}{4+r}$=$\frac{24-2r}{16-{r}^{2}}$,
令12-r=t(10<t<12),e1+2e2=2×$\frac{1}{24-t-\frac{128}{t}}$≥2×$\frac{1}{24-16\sqrt{2}}$
=$\frac{1}{12-8\sqrt{2}}$=$\frac{3+2\sqrt{2}}{4}$.
故答案为:$\frac{3+2\sqrt{2}}{4}$.
点评 本题考查了两圆相切的性质、椭圆的性质,主要是椭圆的离心率,考查基本不等式的运用:求最值,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.4位同学各自在阳光体育时间活动,可以选择足球和篮球两项运动中一项,则这两项活动都有同学选择的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{7}{8}$ |
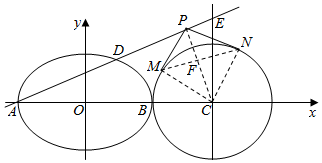 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),A、B分别其左右顶点,直线AE交其右准线CE于点E,交椭圆于点D($\frac{1}{e}$,3),其中e为椭圆的离心率,B为线段OC的中点.圆C是以C点为圆心,CB长为半径的圆,P为直线AE上任意一点,过P向圆C作切线,切点分别为M、N.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),A、B分别其左右顶点,直线AE交其右准线CE于点E,交椭圆于点D($\frac{1}{e}$,3),其中e为椭圆的离心率,B为线段OC的中点.圆C是以C点为圆心,CB长为半径的圆,P为直线AE上任意一点,过P向圆C作切线,切点分别为M、N. 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$离心率为$e=\frac{{\sqrt{3}}}{2}$,以原点为圆心,以椭圆C的短半轴长为半径的圆O与直线l1:$y=x+\sqrt{2}$相切.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$离心率为$e=\frac{{\sqrt{3}}}{2}$,以原点为圆心,以椭圆C的短半轴长为半径的圆O与直线l1:$y=x+\sqrt{2}$相切.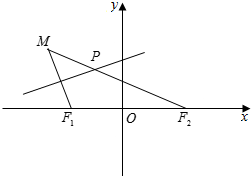 如图所示,点F1(-1,0),F2(1,0),动点M到点F2的距离是$2\sqrt{2}$,线段MF1的中垂线交MF2于点P.
如图所示,点F1(-1,0),F2(1,0),动点M到点F2的距离是$2\sqrt{2}$,线段MF1的中垂线交MF2于点P.