题目内容
1.已知点F1,F2为椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点,若椭圆上存在点P使得$|{\overrightarrow{P{F_1}}}|=2|{\overrightarrow{P{F_2}}}|$,则此椭圆的离心率的取值范围是( )| A. | (0,$\frac{1}{3}$) | B. | (0,$\frac{1}{2}$] | C. | ($\frac{1}{3}$,$\frac{1}{2}$] | D. | [$\frac{1}{3}$,1) |
分析 由题意可得|$\overrightarrow{P{F}_{1}}$|=$\frac{4a}{3}$,|$\overrightarrow{P{F}_{2}}$|=$\frac{2a}{3}$,当P与两焦点F1,F2能构成三角形时,由余弦定理可得ac的不等式,可得离心率的范围;当P与两焦点F1,F2共线时,可e=$\frac{c}{a}$=$\frac{1}{3}$;综合可得.
解答 解:由题意设$|{\overrightarrow{P{F_1}}}|=2|{\overrightarrow{P{F_2}}}|$=2x,则2x+x=2a,
解得x=$\frac{2a}{3}$,故|$\overrightarrow{P{F}_{1}}$|=$\frac{4a}{3}$,|$\overrightarrow{P{F}_{2}}$|=$\frac{2a}{3}$,
当P与两焦点F1,F2能构成三角形时,由余弦定理可得
4c2=$\frac{16{a}^{2}}{9}$+$\frac{4{a}^{2}}{9}$-2×$\frac{4a}{3}$×$\frac{2a}{3}$×cos∠F1PF2,
由cos∠F1PF2∈(-1,1)可得4c2=$\frac{20{a}^{2}}{9}$-$\frac{16{a}^{2}}{9}$cos∠F1PF2∈($\frac{4{a}^{2}}{9}$,$\frac{36{a}^{2}}{9}$),
即$\frac{4{a}^{2}}{9}$<4c2<$\frac{36{a}^{2}}{9}$,∴$\frac{1}{9}$<$\frac{{c}^{2}}{{a}^{2}}$<1,即$\frac{1}{9}$<e2<1,∴$\frac{1}{3}$<e<1;
当P与两焦点F1,F2共线时,可得a+c=2(a-c),解得e=$\frac{c}{a}$=$\frac{1}{3}$;
综上可得此椭圆的离心率的取值范围为[$\frac{1}{3}$,1)
故选:D
点评 本题考查椭圆的简单性质,涉及余弦定理和不等式的性质以及分类讨论的思想,属中档题.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{7}{8}$ |
 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$离心率为$e=\frac{{\sqrt{3}}}{2}$,以原点为圆心,以椭圆C的短半轴长为半径的圆O与直线l1:$y=x+\sqrt{2}$相切.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$离心率为$e=\frac{{\sqrt{3}}}{2}$,以原点为圆心,以椭圆C的短半轴长为半径的圆O与直线l1:$y=x+\sqrt{2}$相切.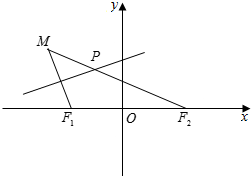 如图所示,点F1(-1,0),F2(1,0),动点M到点F2的距离是$2\sqrt{2}$,线段MF1的中垂线交MF2于点P.
如图所示,点F1(-1,0),F2(1,0),动点M到点F2的距离是$2\sqrt{2}$,线段MF1的中垂线交MF2于点P.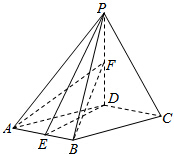 已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=2,点E为AB中点,点F为PD中点.
已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=2,点E为AB中点,点F为PD中点. 已知O为坐标原点,F为椭圆C:x2+$\frac{y^2}{2}$=1在y轴正半轴上的焦点,过F且斜率为-$\sqrt{2}$的直线l与C交与A、B两点,四边形OAPB为平行四边形.
已知O为坐标原点,F为椭圆C:x2+$\frac{y^2}{2}$=1在y轴正半轴上的焦点,过F且斜率为-$\sqrt{2}$的直线l与C交与A、B两点,四边形OAPB为平行四边形.