题目内容
5.变量x,y满足约束条件$\left\{\begin{array}{l}x+y-2≥0\\ x-y-2≤0\\ y≥1\end{array}\right.$,则目标函数z=x+3y的最小值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 先根据约束条件画出可行域,再利用几何意义求最值,z=x+3y表示直线在y轴上的截距,只需求出可行域直线在y轴上的截距最值即可.
解答  解:变量x,y满足约束条件$\left\{\begin{array}{l}x+y-2≥0\\ x-y-2≤0\\ y≥1\end{array}\right.$,画出图形:
解:变量x,y满足约束条件$\left\{\begin{array}{l}x+y-2≥0\\ x-y-2≤0\\ y≥1\end{array}\right.$,画出图形:
目标函数z=x+3y经过点A(1,1),
z在点A处有最小值:z=1+3×1=4,
故选:C.
点评 本题主要考查了简单的线性规划,将可行域各角点的值一一代入,最后比较,即可得到目标函数的最优解,是常用的一种方法.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
13.“x>2“是“x2+2x-8>0“成立的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.4位同学各自在阳光体育时间活动,可以选择足球和篮球两项运动中一项,则这两项活动都有同学选择的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{7}{8}$ |
15. 为迎接即将举行的集体跳绳比赛,高一年级对甲、乙两个代表队各进行了6轮测试,
为迎接即将举行的集体跳绳比赛,高一年级对甲、乙两个代表队各进行了6轮测试,
测试成绩(单位:次/分钟)如表:
(Ⅰ)补全茎叶图并指出乙队测试成绩的中位数和众数;
(Ⅱ)试用统计学中的平均数、方差知识对甲乙两个代表队的测试成绩进行分析.
 为迎接即将举行的集体跳绳比赛,高一年级对甲、乙两个代表队各进行了6轮测试,
为迎接即将举行的集体跳绳比赛,高一年级对甲、乙两个代表队各进行了6轮测试,测试成绩(单位:次/分钟)如表:
| 轮次 | 一 | 二 | 三 | 四 | 五 | 六 |
| 甲 | 73 | 66 | 82 | 72 | 63 | 76 |
| 乙 | 83 | 75 | 62 | 69 | 75 | 68 |
(Ⅱ)试用统计学中的平均数、方差知识对甲乙两个代表队的测试成绩进行分析.
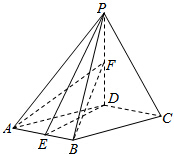 已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=2,点E为AB中点,点F为PD中点.
已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=2,点E为AB中点,点F为PD中点.