题目内容
11.方程组$\left\{\begin{array}{l}{ax-y=0}\\{x-(2a-1)y=1}\end{array}\right.$有且只有一个解,则a的取值范围为( )| A. | (-∞,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1)∪(1,+∞) | B. | (-∞,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,+∞) | ||
| C. | (-∞,1)∪(1,+∞) | D. | R |
分析 化简消元可得x-(2a-1)ax=1,从而可得1-2a2+a≠0,从而解得.
解答 解:化简方程组$\left\{\begin{array}{l}{ax-y=0}\\{x-(2a-1)y=1}\end{array}\right.$得,
x-(2a-1)ax=1,
即x(1-2a2+a)=1,
故1-2a2+a≠0,
解得,a≠1且a≠-$\frac{1}{2}$;
当a≠1且a≠-$\frac{1}{2}$时,
x=$\frac{1}{1+a-2{a}^{2}}$,y=a$\frac{1}{1+a-2{a}^{2}}$,
即有且只有一个解;
故a的取值范围为
(-∞,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1)∪(1,+∞),
故选A.
点评 本题考查了方程的解法与应用,同时考查了方程思想与综合法的应用.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
1.式子$\frac{1}{{2-{{cos}^2}θ}}$+$\frac{1}{{2-{{sin}^2}θ}}$(θ∈R)的最小值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
19.设随机变量X服从正态分布N(2,22),则P(2<X<3)可以表示为( )
| A. | 1~P(X<1) | B. | $\frac{1-2P(X<1)}{2}$ | C. | P(0<X<1) | D. | $\frac{1+2P(X<1)}{2}$ |
16.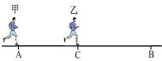 如图所示,甲从A地由静止匀加速跑向B地,当甲前进距离为x1时,乙从距A地x2处的C点由静止出发,加速度与甲相同,最后二人同时到达B地,则AB两地距离为( )
如图所示,甲从A地由静止匀加速跑向B地,当甲前进距离为x1时,乙从距A地x2处的C点由静止出发,加速度与甲相同,最后二人同时到达B地,则AB两地距离为( )
 如图所示,甲从A地由静止匀加速跑向B地,当甲前进距离为x1时,乙从距A地x2处的C点由静止出发,加速度与甲相同,最后二人同时到达B地,则AB两地距离为( )
如图所示,甲从A地由静止匀加速跑向B地,当甲前进距离为x1时,乙从距A地x2处的C点由静止出发,加速度与甲相同,最后二人同时到达B地,则AB两地距离为( )| A. | x1+x2 | B. | $\frac{({x}_{1}+{x}_{2})^{2}}{4{x}_{1}}$ | ||
| C. | $\frac{{x}_{1}^{2}}{4({x}_{1}+{x}_{2})}$ | D. | $\frac{({x}_{1}+{x}_{2})^{2}}{({x}_{1}-{x}_{2}){x}_{1}}$ |
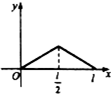
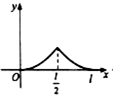
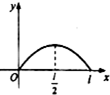
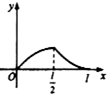
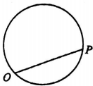 如图,点P从点O出发,按逆时针方向沿周长为l的圆周运动一周,则O,P两点连线的距离y与点P走过的路程x的函数图象可能是( )
如图,点P从点O出发,按逆时针方向沿周长为l的圆周运动一周,则O,P两点连线的距离y与点P走过的路程x的函数图象可能是( )