题目内容
2.设an(n=2,3,4…)是(3+$\sqrt{x}$)n的展开式中x的一次项的系数,则$\frac{2016}{2015}$($\frac{3^2}{a_2}$+$\frac{3^3}{a_3}$+…+$\frac{{3^{2016}}}{{a_{2016}}}$)的值是18.分析 (3+$\sqrt{x}$)n的展开式中,Tr+1=${∁}_{n}^{r}{3}^{n-r}(\sqrt{x})^{r}$,令r=2,则T3=${∁}_{n}^{2}{3}^{n-2}x$,根据an(n=2,3,4…)是(3+$\sqrt{x}$)n的展开式中x的一次项的系数,可得an=${∁}_{n}^{2}$3n-2,即$\frac{{3}^{n}}{{a}_{n}}$=$\frac{9}{{∁}_{n}^{2}}$=18$(\frac{1}{n-1}-\frac{1}{n})$.再利用“裂项求和”方法即可得出.
解答 解:(3+$\sqrt{x}$)n的展开式中,Tr+1=${∁}_{n}^{r}{3}^{n-r}(\sqrt{x})^{r}$,
令r=2,则T3=${∁}_{n}^{2}{3}^{n-2}x$,
∵an(n=2,3,4…)是(3+$\sqrt{x}$)n的展开式中x的一次项的系数,
∴an=${∁}_{n}^{2}$3n-2,
∴$\frac{{3}^{n}}{{a}_{n}}$=$\frac{9}{{∁}_{n}^{2}}$=18$(\frac{1}{n-1}-\frac{1}{n})$.
∴$\frac{2016}{2015}$($\frac{3^2}{a_2}$+$\frac{3^3}{a_3}$+…+$\frac{{3^{2016}}}{{a_{2016}}}$)=$\frac{2016}{2015}×18[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{2015}-\frac{1}{2016})]$=$\frac{2016}{2015}×18×(1-\frac{1}{2016})$=18,
故答案为:18.
点评 本题考查了二项式定理的应用、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | 1 |
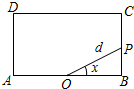 如图,已知矩形ABCD中,AB=2,BC=1,O为线段AB的中点,动点P从B出发,沿矩形ABCD的边逆时针运动,运动至A点时终止.设∠BOP=x,OP=d,将d表示为x的函数d=f(x).则下列命题中:
如图,已知矩形ABCD中,AB=2,BC=1,O为线段AB的中点,动点P从B出发,沿矩形ABCD的边逆时针运动,运动至A点时终止.设∠BOP=x,OP=d,将d表示为x的函数d=f(x).则下列命题中:①f(x)有最小值1;
②f(x)有最大值$\sqrt{2}$;
③f(x)有3个极值点;
④f(x)有4个单调区间.
其中正确的是( )
| A. | ①② | B. | ②③ | C. | ①②④ | D. | ①②③④ |
| A. | (-∞,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1)∪(1,+∞) | B. | (-∞,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,+∞) | ||
| C. | (-∞,1)∪(1,+∞) | D. | R |
 如图,已知平行于圆柱轴的截面ABB1A1是正方形,面积为3a2,它与轴的距离是底面半径的一半,求圆柱的全面积和体积.
如图,已知平行于圆柱轴的截面ABB1A1是正方形,面积为3a2,它与轴的距离是底面半径的一半,求圆柱的全面积和体积.