题目内容
6.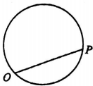 如图,点P从点O出发,按逆时针方向沿周长为l的圆周运动一周,则O,P两点连线的距离y与点P走过的路程x的函数图象可能是( )
如图,点P从点O出发,按逆时针方向沿周长为l的圆周运动一周,则O,P两点连线的距离y与点P走过的路程x的函数图象可能是( )| A. | 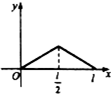 | B. | 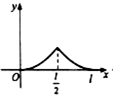 | C. | 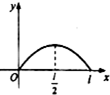 | D. | 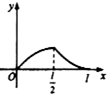 |
分析 首先根据题意求出圆的半径,进一步利用弦与所对的弧长之间的关系建立等量,求出结果,可得结论.
解答 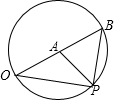 解:已知圆的周长为l,则设圆的半径为r,则:l=2πr
解:已知圆的周长为l,则设圆的半径为r,则:l=2πr
所以:r=$\frac{l}{2π}$
设O,P两点连线的距离为y,点P走过的路程为x,连接AP,设∠OAP=θ,
则:x=$\frac{l}{2π}$θ
整理得:$\frac{θ}{2}=\frac{πx}{l}$
利用sin$\frac{θ}{2}$=$\frac{\frac{y}{2}}{\frac{l}{2π}}$=$\frac{πy}{l}$
则:y=$\frac{l}{π}sin(\frac{πx}{l})$.
故选:C.
点评 本题考查的知识要点:弧长关系式的应用,及相关的运算问题,考查数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
1.在(2a-3b)n的展开式中第4项与第8项的二项式系数相等,则展开式共有( )
| A. | 13项 | B. | 12项 | C. | 11项 | D. | 10项 |
11.方程组$\left\{\begin{array}{l}{ax-y=0}\\{x-(2a-1)y=1}\end{array}\right.$有且只有一个解,则a的取值范围为( )
| A. | (-∞,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1)∪(1,+∞) | B. | (-∞,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,+∞) | ||
| C. | (-∞,1)∪(1,+∞) | D. | R |
16.首项为a(a≠0)的数列{an},既是等差数列,又是等比数列,则这个数列的前n项和为( )
| A. | an-1 | B. | na | C. | an | D. | (n-1)a |