题目内容
已知函数f(x)=x2-1在点P(1,0)处的倾斜角为α,则sin(2a+
)= .
| π |
| 4 |
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用,三角函数的求值
分析:求出函数的导数,利用导数的几何意义即可得到结论.
解答:
解:函数的导数为f′(x)=2x,
则函数f(x)=x2-1在点P(1,0)处的斜率k=f′(1)=2,
则tanα=2,解得sinα=
,cosα=
,
则sin2α=2sinαcosα=2×
×
=
,cos2α=2cos2α-1=2×(
)2-1=-
,
则sin(2a+
)=sin2acos
+cos2acos
=
(sin2a+cos2a)=
(
-
)=
×
=
,
故答案为:
则函数f(x)=x2-1在点P(1,0)处的斜率k=f′(1)=2,
则tanα=2,解得sinα=
2
| ||
| 5 |
| ||
| 5 |
则sin2α=2sinαcosα=2×
2
| ||
| 5 |
| ||
| 5 |
| 4 |
| 5 |
| ||
| 5 |
| 3 |
| 5 |
则sin(2a+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| 4 |
| 5 |
| 3 |
| 5 |
| ||
| 2 |
| 1 |
| 5 |
| ||
| 10 |
故答案为:
| ||
| 10 |
点评:本题主要考查导数的几何意义以及两角和的正弦公式的应用,综合考查学生的计算能力.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
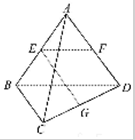 如图:已知空间四边形ABCD的边长和对角线的长都为2,点E,F,G分别是AB,AD,DC的中点求下列数量积:
如图:已知空间四边形ABCD的边长和对角线的长都为2,点E,F,G分别是AB,AD,DC的中点求下列数量积: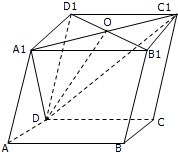 如图所示,在平行六面体ABCD-A1B1C1D1中,O是B1D1的中点,求证:
如图所示,在平行六面体ABCD-A1B1C1D1中,O是B1D1的中点,求证: