题目内容
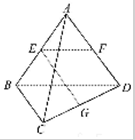如图：已知空间四边形ABCD的边长和对角线的长都为2，点E，F，G分别是AB，AD，DC的中点求下列数量积：（1）
| AB |
| AC |
（2）
| AD |
| BD |
（3）
| GF |
| AC |
（4）
| EF |
| BC |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由题意，四面体时正四面体，每个三角形是等边三角形，利用向量的数量积的定义解答．
解答：
解：由于空间四边形ABCD的边长和对角线的长都为2，点E，F，G分别是AB，AD，DC的中点，
故（1）
•
=2×2×cos60°=2，
（2）
•
=2×2×cos60°=2，
（3）
•
=
•
•
=
×2×2=2，
（4）
•
=
•
•
=
×2×2×cos60°=1．
故（1）
| AB |
| AC |
（2）
| AD |
| BD |
（3）
| GF |
| AC |
| 1 |
| 2 |
| AC |
| AC |
| 1 |
| 2 |
（4）
| EF |
| BC |
| 1 |
| 2 |
| BD |
| BC |
| 1 |
| 2 |
点评：本题考查了平面向量的数量积定义；正确运用数量积公式，注意向量的夹角大小时解答的关键，属于基础题
练习册系列答案
相关题目
函数f（x）=
+
的定义域为（ ）
| 1 |
| ln(x+2) |
| 9-x2 |
| A、[-3，-1）∪（-1，3] |
| B、（-2，-1）∪（-1，3] |
| C、[-3，3] |
| D、（-2，3] |