题目内容
已知f(α)=
.
(1)化简f(α);
(2)若α为第三象限角,且cos(
-α)=
,求f(α)的值.
sin(
| ||
| tam(-α)sin(π-α) |
(1)化简f(α);
(2)若α为第三象限角,且cos(
| 3π |
| 2 |
| 1 |
| 5 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:(1)利用诱导公式可化简f(α)=-cosα.
(2)依题意,可得sinα=-
,利用同角三角函数间的关系式可得cosα=-
=-
,从而可得答案.
(2)依题意,可得sinα=-
| 1 |
| 5 |
| 1-sin2α |
2
| ||
| 5 |
解答:
解:(1)f(α)=
=
=-cosα;
(2)∵α为第三象限角,且cos(
-α)=-sinα=
,
∴sinα=-
,∴cosα=-
=-
,
∴f(α)=-cosα=
.
sin(
| ||
| tan(-α)sin(π-α) |
| cosα•(-sinα)•(-tanα) |
| -tanαsinα |
(2)∵α为第三象限角,且cos(
| 3π |
| 2 |
| 1 |
| 5 |
∴sinα=-
| 1 |
| 5 |
| 1-sin2α |
2
| ||
| 5 |
∴f(α)=-cosα=
2
| ||
| 5 |
点评:本题考查运用诱导公式化简求值,考查同角三角函数间的关系式的应用,属于中档题.

练习册系列答案
相关题目
直线l1、l2的方向向量分别为
=(1,2,-2),
=(-2,3,2),则( )
| a |
| b |
| A、l1∥l2 |
| B、l1与l2相交,但不垂直 |
| C、l1⊥l2 |
| D、不能确定 |
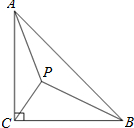 如图所示,△ABC为直角三角形,CA=
如图所示,△ABC为直角三角形,CA=