Question

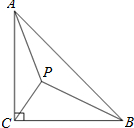如图所示，△ABC为直角三角形，CA=

3

，BC=1，P为△ABC内一点，满足∠BPC=90°，∠APC=150°，求tan∠PCA．

Answer 1

考点：两角和与差的正切函数

专题：计算题,解三角形

分析：设∠PCA=α，在Rt△PBC中，可得PC=sinα，在△PAC中，由正弦定理得

AC

sin∠APC

=

PC

sin∠PAC

，即

3

sin150°

=

sinα

sin(30°-α)

，化简即可求出．

解答： 解：设∠PCA=α，在Rt△PBC中，PC=BCcos（90°-α）=sinα，
在△PAC中，由正弦定理得

AC

sin∠APC

=

PC

sin∠PAC

，
即

3

sin150°

=

sinα

sin(30°-α)

，
化为

3

cosα=4sinα，
可得tanα=

3

4

．

点评：本题主要考查了正弦定理的应用，熟练掌握直角三角形的边角关系、正弦定理和余弦定理的应用是解题的关键，属于中档题．