题目内容
已知函数f(x)=-4lnx-
ax2+x,其中a∈R.
(Ⅰ)若a=-
,求函数f(x)的最小值;
(Ⅱ)若存在两个整数m,n,使得函数f(x)在区间(m,n)上是增函数,且(m,n)⊆(0,a+4),求n的最大值,及n取最大值时a的取值范围.
| 1 |
| 2 |
(Ⅰ)若a=-
| 1 |
| 2 |
(Ⅱ)若存在两个整数m,n,使得函数f(x)在区间(m,n)上是增函数,且(m,n)⊆(0,a+4),求n的最大值,及n取最大值时a的取值范围.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)先求f(x),f′(x),找函数f(x)的单调区间,判断它的单调性,从而求出f(x)的最小值.
(Ⅱ)先根据(m,n)⊆(0,a+4),得到:0≤m<n≤a+4,a>-4.求f′(x)=
,设h(x)=-ax2+x-4,根据已知条件,h(x)>0在(m.n)上恒成立.这时候,讨论a的取值情况,从而得出a的取值范围,并求出n的最大值.
(Ⅱ)先根据(m,n)⊆(0,a+4),得到:0≤m<n≤a+4,a>-4.求f′(x)=
| -ax2+x-4 |
| x |
解答:
解:(Ⅰ)f(x)=-4lnx+
x2+x,f′(x)=-
+
x+1=
(x>0);
∴x∈(0,2)时,f′(x)<0;x∈(2,+∞)时,f′(x)>0;
∴f(x)min=f(2)=-4ln2+3.
(Ⅱ)∵(m,n)⊆(0,a+4),∴0≤m<n≤a+4,a>-4 ①;
f′(x)=-
-ax+1=
(x>0),
设h(x)=-ax2+x-4,则:
f′(x)>0,即h(x)>0,对x∈(m,n)恒成立.
(1)当a<0时,∵h(0)=-4,∴h(a+4)=-a[(a+4)2-1]>0,解得a>-3,或a<-5 ②;
由①②得:-3<a<0,m<n≤a+4<4;
又m,n为整数,∴m<n≤3;
当且仅当
,即-1≤a≤-
时,nmax=3;
(2)当a=0时,f(x)的递增区间是[4,+∞),不适合条件;
(3)当a>0时,由h(0)<0,h(a+4)<0,要使f′(x)>0在(0,a+4)上有解,则:
,不等式组无解,∴不适合条件.
综上:nmax=3,此时a的取值范围是:[-1,-
].
| 1 |
| 4 |
| 4 |
| x |
| 1 |
| 2 |
| (x+4)(x-2) |
| 2x |
∴x∈(0,2)时,f′(x)<0;x∈(2,+∞)时,f′(x)>0;
∴f(x)min=f(2)=-4ln2+3.
(Ⅱ)∵(m,n)⊆(0,a+4),∴0≤m<n≤a+4,a>-4 ①;
f′(x)=-
| 4 |
| x |
| -ax2+x-4 |
| x |
设h(x)=-ax2+x-4,则:
f′(x)>0,即h(x)>0,对x∈(m,n)恒成立.
(1)当a<0时,∵h(0)=-4,∴h(a+4)=-a[(a+4)2-1]>0,解得a>-3,或a<-5 ②;
由①②得:-3<a<0,m<n≤a+4<4;
又m,n为整数,∴m<n≤3;
当且仅当
|
| 1 |
| 2 |
(2)当a=0时,f(x)的递增区间是[4,+∞),不适合条件;
(3)当a>0时,由h(0)<0,h(a+4)<0,要使f′(x)>0在(0,a+4)上有解,则:
|
综上:nmax=3,此时a的取值范围是:[-1,-
| 1 |
| 2 |
点评:考查导数符号和函数单调性的关系,以及函数单调性和函数最值的关系,而对于第二问,求解的思路就是,求整数n的取值范围,从而求出n的最大值,及此时a的取值范围.

练习册系列答案
相关题目
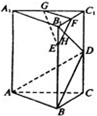 如图在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,E是BB1上的一点,且EB1=1,D、F、G分别是CC1、B1C1、A1C1的中点,EF与B1D相交于H.
如图在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,E是BB1上的一点,且EB1=1,D、F、G分别是CC1、B1C1、A1C1的中点,EF与B1D相交于H.