题目内容
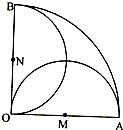 如图,在圆心角为直角的扇形OAB区域中,M、N分别为OA、OB的中点,在M、N两点处各有一个通信基站,其信号的覆盖范围分别为以OA、OB为直径的圆,在扇形OAB内随机取一点,则此点无信号的概率是( )
如图,在圆心角为直角的扇形OAB区域中,M、N分别为OA、OB的中点,在M、N两点处各有一个通信基站,其信号的覆盖范围分别为以OA、OB为直径的圆,在扇形OAB内随机取一点,则此点无信号的概率是( )A、1-
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:几何概型
专题:应用题,概率与统计
分析:OA的中点是M,则∠CMO=90°,这样就可以求出弧OC与弦OC围成的弓形的面积,从而可求出两个圆的弧OC围成的阴影部分的面积,用扇形OAB的面积减去三角形的面积,减去加上两个弧OC围成的面积就是无信号部分的面积,最后根据几何概型的概率公式解之即可.
解答:
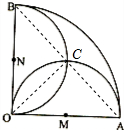 解:OA的中点是M,则∠CMO=90°,半径为OA=r
解:OA的中点是M,则∠CMO=90°,半径为OA=r
S扇形OAB=
πr2,S半圆OAC=
π(
)2=
πr2,
S△OmC=
×
×
=
r2,
S弧OC=
S半圆OAC-S△ODC=
πr2-
r2,
两个圆的弧OC围成的阴影部分的面积为
πr2-
r2,
图中无信号部分的面积为
πr2-
r2-(
πr2-
r2)=
πr2-
r2,
∴无信号部分的概率是:
-
.
故选:A.
 解:OA的中点是M,则∠CMO=90°,半径为OA=r
解:OA的中点是M,则∠CMO=90°,半径为OA=rS扇形OAB=
| 1 |
| 4 |
| 1 |
| 2 |
| r |
| 2 |
| 1 |
| 8 |
S△OmC=
| 1 |
| 2 |
| r |
| 2 |
| r |
| 2 |
| 1 |
| 8 |
S弧OC=
| 1 |
| 2 |
| 1 |
| 16 |
| 1 |
| 8 |
两个圆的弧OC围成的阴影部分的面积为
| 1 |
| 8 |
| 1 |
| 4 |
图中无信号部分的面积为
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 4 |
∴无信号部分的概率是:
| 1 |
| 2 |
| 1 |
| π |
故选:A.
点评:本题主要考查了几何概型,解题的关键是求无信号部分的面积,不规则图形的面积可以转化为几个不规则的图形的面积的和或差的计算,属于中档题.

练习册系列答案
相关题目
若向量
=(1,-2),
=(2,1),
=(-4,-2),则下列说法中错误的是( )
| a |
| b |
| c |
A、
| ||||||||
B、向量
| ||||||||
C、
| ||||||||
D、对同一平面内的任意向量
|
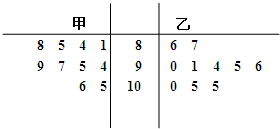 甲、乙两所学校高三级某学年10次联合考试的理科数学成绩平均分用茎叶图如图所示,则甲乙两所学校的平均分
甲、乙两所学校高三级某学年10次联合考试的理科数学成绩平均分用茎叶图如图所示,则甲乙两所学校的平均分. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图所示的程序框图表示求算式“2×3×5×9×17”之值,则判断框内不能填入( )


| A、k≤17? | B、k≤23 |
| C、k≤28? | D、k≤33? |