题目内容
函数f（x）=|log2x|+x-2的零点个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：将方程的解的个数转化为两个函数的交点问题，通过图象一目了然．
解答：
解：函数f（x）=|log2x|+x-2的零点个数，就是方程|log2x|+x-2=0的根的个数，
得|log2x|=2-x，
令f（x）=|log2x|，g（x）=2-x，
画出函数的图象，如图：
由图象得：f（x）与g（x）有2个交点，
∴方程|log2x|+x-2=0解的个数为2个，
故选：B．
解：函数f（x）=|log2x|+x-2的零点个数，就是方程|log2x|+x-2=0的根的个数，得|log2x|=2-x，
令f（x）=|log2x|，g（x）=2-x，
画出函数的图象，如图：
由图象得：f（x）与g（x）有2个交点，
∴方程|log2x|+x-2=0解的个数为2个，
故选：B．
点评：本题考查了函数根的存在性问题，考查转化思想，数形结合思想，是一道基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知在?ABCD中，点M在AB上，且AM=3MB，点N在BD上，且
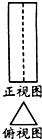某几何体的正视图和俯视图如图所示，若正视图是面积为3的矩形，俯视图是边长为1的正三角形，则该几何体的侧视图的面积为（ ）| A、3 | ||||
B、3
| ||||
C、
| ||||
| D、9 |
如图所示的程序框图表示求算式“2×3×5×9×17”之值，则判断框内不能填入（ ）
| A、k≤17？ | B、k≤23 |
| C、k≤28？ | D、k≤33？ |
若实数x，y满足条件
，则z=x+y的最大值为（ ）
|
| A、2 | ||
| B、4 | ||
C、2
| ||
| D、6 |