题目内容
对于任意实数x,符号[x]表示x的整数部分,即[x]是不超过x的最大整数.在数轴上[x]是在点x左侧的第一个整数点,当x是整数时,[x]就是x,这个函数[x]叫做“取整函数”.它在数学本身和生产实践中有着广泛的应用.那么[log31]+[log32]+[log33]+…[log310]= .
考点:数列的求和
专题:函数的性质及应用
分析:由已知得[log31]+[log32]=0,[log33]=[log34]=[log35]=[log36]=[log37]=[log38]=1,[log39]=[log310]=2.
解答:
解:由题意得:
[log31]+[log32]+[log33]+…[log310]
=0+0+1+1+1+1+1+1+2+2
=10.
故答案为:10.
[log31]+[log32]+[log33]+…[log310]
=0+0+1+1+1+1+1+1+2+2
=10.
故答案为:10.
点评:本题考查数列的前10项和的求法,是基础题,解题时要注意对数性质和取整函数的性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某程序框图如图,当输入x=3时,则输出的y=( )


| A、1 | B、2 | C、4 | D、8 |
函数f(x)的图象如图所示,下列数值排序正确的是( )
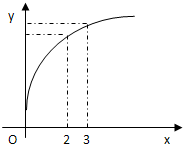

| A、0<f′(3)<f(3)-f(2)<f′(2) |
| B、0<f′(2)<f′(3)<f(3)-f(2) |
| C、0<f′(3)<f′(2)<f(3)-f(2) |
| D、0<f(3)-f(2)<f′(2)<f′(3) |
若方程4x+(m-3)•2x+m=0有两个不相同的实根,则实数m的取值范围是( )
| A、m>0 | B、m>1 |
| C、0≤m≤1 | D、0<m<1 |
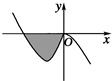 已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围区域(图中阴影部分)的面积为
已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围区域(图中阴影部分)的面积为 如图,三棱柱ABC-A1B1C1中,侧棱与底面垂直,A1B1⊥B1C1,AB=BC=BB1=2,M是BC1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱与底面垂直,A1B1⊥B1C1,AB=BC=BB1=2,M是BC1的中点.