题目内容
设函数f(a)=sinα+
cosα,其中,角α的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤α≤π.
(Ⅰ)若P点的坐标为(-
,1),求f(a)的值;
(Ⅱ)若点P(x,y)为平面区域
上的一个动点,试确定角α的取值范围,并求函数f(a)的最小值及取得最小值时的α的值.
| 3 |
(Ⅰ)若P点的坐标为(-
| 3 |
(Ⅱ)若点P(x,y)为平面区域
|
考点:简单线性规划的应用
专题:三角函数的图像与性质,不等式的解法及应用
分析:(Ⅰ)若P点的坐标为(-
,1),根据三角函数的定义,可得sinα=
,cosα=-
,代入可得f(a)的值;
(Ⅱ)若点P(x,y)为平面区域
上的一个动点,则α∈[
,
],结合正弦函数的图象和性质可得函数f(a)的最小值及取得最小值时的α的值.
| 3 |
| 1 |
| 2 |
| ||
| 2 |
(Ⅱ)若点P(x,y)为平面区域
|
| π |
| 4 |
| π |
| 2 |
解答:
解:(Ⅰ)若P点的坐标为(-
,1),
则sinα=
,cosα=-
,
故f(a)=sinα+
cosα=
-
×
=-1,
(Ⅱ)约束条件
对应的可行域如下图所示:
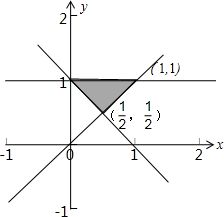
若点P(x,y)为平面区域
上的一个动点,
则α∈[
,
],
∵f(a)=sinα+
cosα=2sin(α+
),
∴α+
∈[
,
],
由y=sinx在[
,
]上为减函数,
故当α+
=
,即α=
时,f(a)取最小值1.
| 3 |
则sinα=
| 1 |
| 2 |
| ||
| 2 |
故f(a)=sinα+
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
(Ⅱ)约束条件
|

若点P(x,y)为平面区域
|
则α∈[
| π |
| 4 |
| π |
| 2 |
∵f(a)=sinα+
| 3 |
| π |
| 3 |
∴α+
| π |
| 3 |
| 7π |
| 12 |
| 5π |
| 6 |
由y=sinx在[
| 7π |
| 12 |
| 5π |
| 6 |
故当α+
| π |
| 3 |
| 5π |
| 6 |
| π |
| 2 |
点评:本题考查的知识点是线性规划,正弦函数的图象和性质,和差角公式,是三角函数与线性规划的综合应用,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设U={x∈N|-2<x≤3},A={3},则∁UA=( )
| A、{-1,0,1,2,3} |
| B、{1,2,3} |
| C、{0,1,2} |
| D、{-1,0,1,2} |
函数f(x)的图象如图所示,下列数值排序正确的是( )
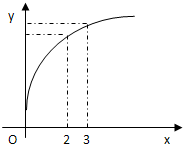

| A、0<f′(3)<f(3)-f(2)<f′(2) |
| B、0<f′(2)<f′(3)<f(3)-f(2) |
| C、0<f′(3)<f′(2)<f(3)-f(2) |
| D、0<f(3)-f(2)<f′(2)<f′(3) |
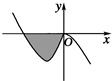 已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围区域(图中阴影部分)的面积为
已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围区域(图中阴影部分)的面积为 如图,三棱柱ABC-A1B1C1中,侧棱与底面垂直,A1B1⊥B1C1,AB=BC=BB1=2,M是BC1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱与底面垂直,A1B1⊥B1C1,AB=BC=BB1=2,M是BC1的中点.