题目内容
定义域为R的四个函数:①y=x2+1 ②y=2x ③y=x3 ④y=2sinx中,奇函数的个数有 (写出正确的序号)
考点:函数奇偶性的判断
专题:计算题,函数的性质及应用
分析:由于定义域为R,关于原点对称,只要判断f(-x)是否等于±f(x),即可判断每个函数的奇偶性,即可得到结论.
解答:
解:对于①,y=x2+1是偶函数,不满足条件;
对于②,y=2x为非奇非偶函数,不满足条件;
对于③,y=x3为奇函数,满足条件;
对于④,y=2sinx为奇函数,满足条件.
故是奇函数的为③④,
故答案为:③④
对于②,y=2x为非奇非偶函数,不满足条件;
对于③,y=x3为奇函数,满足条件;
对于④,y=2sinx为奇函数,满足条件.
故是奇函数的为③④,
故答案为:③④
点评:本题主要考查函数奇偶性的判断,要求熟练掌握常见函数的奇偶性的性质.

练习册系列答案
相关题目
设U={x∈N|-2<x≤3},A={3},则∁UA=( )
| A、{-1,0,1,2,3} |
| B、{1,2,3} |
| C、{0,1,2} |
| D、{-1,0,1,2} |
某程序框图如图,当输入x=3时,则输出的y=( )


| A、1 | B、2 | C、4 | D、8 |
函数f(x)=lg
的定义域为( )
| x2-9 |
| A、[3,+∞) |
| B、(3,+∞) |
| C、(-∞,-3]∪[3,+∞) |
| D、(-∞,-3)∪(3,+∞) |
函数f(x)的图象如图所示,下列数值排序正确的是( )
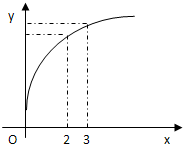

| A、0<f′(3)<f(3)-f(2)<f′(2) |
| B、0<f′(2)<f′(3)<f(3)-f(2) |
| C、0<f′(3)<f′(2)<f(3)-f(2) |
| D、0<f(3)-f(2)<f′(2)<f′(3) |