题目内容
关于x的方程2x2+（m-3）x+2m-1=0有两实根x1，x2，且满足x1＜1＜x2，则m的取值范围为 ．
考点：一元二次方程的根的分布与系数的关系
专题：函数的性质及应用
分析：设f（x）=2x2+（m-3）x+2m-1，则由题意可得：f（0）＜0，解不等式求得实数m的取值范围．
解答：
解：令f（x）=x2+（m-3）x+2m-1，
依题意，f（1）=2+m-3+2m-1＜0，
∴m＜1．
故答案为：（-∞，1）．
依题意，f（1）=2+m-3+2m-1＜0，
∴m＜1．
故答案为：（-∞，1）．
点评：此题主要考查了根与系数的关系，将根与系数的关系与代数式变形相结合解题，是一种经常使用的解题方法．
练习册系列答案
相关题目
函数f（x）的图象如图所示，下列数值排序正确的是（ ）
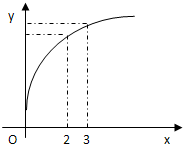
| A、0＜f′（3）＜f（3）-f（2）＜f′（2） |
| B、0＜f′（2）＜f′（3）＜f（3）-f（2） |
| C、0＜f′（3）＜f′（2）＜f（3）-f（2） |
| D、0＜f（3）-f（2）＜f′（2）＜f′（3） |
如图，三棱柱ABC-A1B1C1中，侧棱与底面垂直，A1B1⊥B1C1，AB=BC=BB1=2，M是BC1的中点．