题目内容
已知函数y=x2+(b+1)x+c在(-∞,1)是单调递减函数,则b取值范围是( )
| A、b≥-3 | B、b≤-3 |
| C、b>-3 | D、b<-3 |
考点:二次函数的性质
专题:函数的性质及应用
分析:首先根据函数y=x2+(b+1)x+c求得对称轴方程:x=-
,进一步根据单调区间和对称轴的关系确定结果.
| b+1 |
| 2 |
解答:
解:函数y=x2+(b+1)x+c的对称轴方程为:x=-
∵在x∈(-∞,1)是单调递减
∴-
≥1
解得:b≤-3
故选:B
| b+1 |
| 2 |
∵在x∈(-∞,1)是单调递减
∴-
| b+1 |
| 2 |
解得:b≤-3
故选:B
点评:本题考查的知识要点:二次函数的方程和系数的关系,单调区间和对称轴的关系及解不等式问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
数列{an}中,已知an=2n-17,该数列中相邻两项积为负数的是( )
| A、a6和a7 |
| B、a7和a8 |
| C、a8和a9 |
| D、a9和a10 |
设U={x∈N|-2<x≤3},A={3},则∁UA=( )
| A、{-1,0,1,2,3} |
| B、{1,2,3} |
| C、{0,1,2} |
| D、{-1,0,1,2} |
某程序框图如图,当输入x=3时,则输出的y=( )


| A、1 | B、2 | C、4 | D、8 |
函数f(x)的图象如图所示,下列数值排序正确的是( )
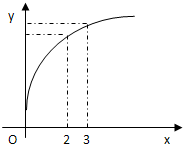

| A、0<f′(3)<f(3)-f(2)<f′(2) |
| B、0<f′(2)<f′(3)<f(3)-f(2) |
| C、0<f′(3)<f′(2)<f(3)-f(2) |
| D、0<f(3)-f(2)<f′(2)<f′(3) |
 如图,定义在[-1,+∞)上的函数f(x)的图象由一条线段及抛物线的一部分组成.
如图,定义在[-1,+∞)上的函数f(x)的图象由一条线段及抛物线的一部分组成.