题目内容
已知向量
=（sinx，1），
=（cosx，-
）
（1）当
⊥
时，求|
+
|的值；
（2）求函数f（x）=
•(
-
)的最小正周期；
（3）已知f（x0）=-
，且x0∈[0．π]，求x0的值．
| a |
| b |
| 1 |
| 2 |
（1）当
| a |
| b |
| a |
| b |
（2）求函数f（x）=
| a |
| b |
| a |
（3）已知f（x0）=-
| 3 |
| 2 |
考点：两角和与差的正弦函数,平面向量数量积的运算,三角函数的周期性及其求法
专题：三角函数的求值,三角函数的图像与性质,平面向量及应用
分析：由已知利用向量的数量积坐标运算求出f（x）的解析式，然后利用三角函数公式化简求周期等．
解答：
解：因为向量
=（sinx，1），
=（cosx，-
）
所以（1）当
⊥
时，
•
=sinxcosx-
=0，所以sin2x=1，|
+
|2=
2+2
•
+
2=sin2x+1+cos2x+
+0=
，
所以|
+
|=
；
（2）函数f（x）=
•(
-
)=
•
-
2=sinxcosx-
-sin2x-1=
sin2x+
cos2x-2=
sin(2x+
)-2，
所以f（x）的最小正周期为T=
=π；
（3）已知f（x0）=-
，由（2）得
sin(2x0+
)-2=-
，所以sin（2x0+
）=
，且x0∈[0．π]，所以2x0+
∈[
，
π]，
所以x0的值为
，
π，
π．
| a |
| b |
| 1 |
| 2 |
所以（1）当
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| a |
| a |
| b |
| b |
| 1 |
| 4 |
| 9 |
| 4 |
所以|
| a |
| b |
| 3 |
| 2 |
（2）函数f（x）=
| a |
| b |
| a |
| a |
| b |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |
所以f（x）的最小正周期为T=
| 2π |
| 2 |
（3）已知f（x0）=-
| 3 |
| 2 |
| ||
| 2 |
| π |
| 4 |
| 3 |
| 2 |
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
| 9 |
| 4 |
所以x0的值为
| π |
| 4 |
| 3 |
| 4 |
| 9 |
| 4 |
点评：本题考查了向量的坐标运算以及三角函数的化简与求值，关键是由向量的坐标运算后，利用三角函数公式将解析式化为一个角的一个三角函数的形式．
练习册系列答案
相关题目
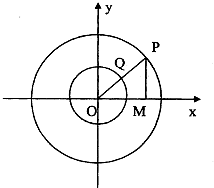以原点为圆心的两个同心圆的方程分别为x2+y2=4和x2+y2=1，过原点O的射线交大圆于点P，交小圆于点Q，作PM⊥x轴于M，若
如图，焦点在x轴的椭圆C：