题目内容
8.正方形ABCD的边长为2,M,N分别是边AB,BC上的点,当△BMN的周长是4时,∠MDN的大小是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 延长BC,作CE=AM,连接DE,则△ADM≌△DEC,再证明△MND≌△DNE,即可得到结论.
解答 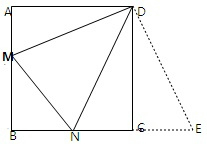 解:延长BC,作CE=AM,连接DE,则△ADM≌△DEC,
解:延长BC,作CE=AM,连接DE,则△ADM≌△DEC,
∴∠ADM=∠CDE,AD=CD,DM=DE,
∴∠MDE=∠MDC+∠CDE=∠MDC+∠ADM=$\frac{π}{2}$,
设AM=x,NC=y,则BM=2-x,BN=2-y,NE=CN+CE=x+y,
MN=△BMN周长-DB-BN=4-(2-x)-(2-y)=x+y=NE,
∴△MND≌△NDE (SSS),
∴∠MDN=∠NDE,
∴∠MDN=$\frac{1}{2}×$$\frac{π}{2}$=$\frac{π}{4}$.
故选:B.
点评 本题考查三角形的全等,考查学生数形结合思想和分析问题、解决问题的能力,属于中档题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
18.已知梯形ABCD中,AB⊥AD,$\overrightarrow{AB}=3\overrightarrow{DC},cos∠DAC=\frac{{\sqrt{3}}}{2},\overrightarrow{BE}=m\overrightarrow{BC}$(0<m<1),若|$\overrightarrow{AE}$|2=$|{\overrightarrow{AC}}||{\overrightarrow{AB}}$|,则$\frac{CE}{CB}$=( )
| A. | $\frac{1+\sqrt{15}}{7}$ | B. | $\frac{1}{7}$ | C. | $\frac{2}{3}$ | D. | $\frac{2+\sqrt{15}}{7}$ |
16.为使高三同学在高考复习中更好的适应全国卷,进一步提升成绩,济南外国语学校计划聘请北京命题组专家利用周四下午第一、二、三节课举办语文、数学、英语、理综4科的专题讲座,每科一节课,每节至少有一科,且数学、理综不安排在同一节,则不同的安排方法共有( )
| A. | 36种 | B. | 30种 | C. | 24种 | D. | 6种 |
3.若关于x的不等式x2-mx<0的解集为{x|0<x<2},则m的值为( )
| A. | 1 | B. | 2 | C. | -1 | D. | 3 |
20.计算$C_5^4+C_6^4+C_7^4+C_8^4$等于( )
| A. | 125 | B. | 126 | C. | 120 | D. | 132 |
18.过直线x+y+1=0与2x-y-4=0的交点,且一个方向向量$\overrightarrow v=({-1,3})$的直线方程是( )
| A. | 3x+y-1=0 | B. | x+3y-5=0 | C. | 3x+y-3=0 | D. | x+3y+5=0 |
 已知△ABC中,顶点A(7,-3),AC边上的高BH所在直线方程为x-2y-5=0,AB边上的中线CM所在的直线方程为6x-y-21=0.
已知△ABC中,顶点A(7,-3),AC边上的高BH所在直线方程为x-2y-5=0,AB边上的中线CM所在的直线方程为6x-y-21=0.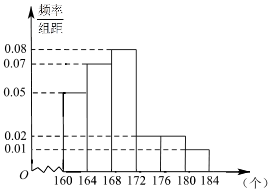 《汉字听写大会》不断创收视新高,为了避免“书写危机”弘扬传统文化,某市对全市10万名市民进行了汉字听写测试,调查数据显示市民的成绩服从正态分布N(168,16).现从某社区居民中随机抽取50名市民进行听写测试,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第一组[160,164),第二组[164,168),…,第六组[180,184),如图是按上述分组方法得到的频率分布直方图.
《汉字听写大会》不断创收视新高,为了避免“书写危机”弘扬传统文化,某市对全市10万名市民进行了汉字听写测试,调查数据显示市民的成绩服从正态分布N(168,16).现从某社区居民中随机抽取50名市民进行听写测试,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第一组[160,164),第二组[164,168),…,第六组[180,184),如图是按上述分组方法得到的频率分布直方图.