题目内容
9.复数z=$\frac{-4+i}{-i}$的共轭复数是( )| A. | -1+4i | B. | -1-4i | C. | 1+4i | D. | 1-4i |
分析 利用复数的代数形式的乘除运算法则先求出z,由此能求出复数z的共轭复数.
解答 解:z=$\frac{-4+i}{-i}$=$\frac{(-4+i)i}{-{i}^{2}}$=-1-4i,
∴复数z=$\frac{-4+i}{-i}$的共轭复数是-1+4i.
故选:A.
点评 本题考查共轭复数的求法,涉及到共轭复数、复数的代数形式的乘除运算法则等基础知识,考查推理论证能力、运算求解能力,是基础题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
17.复数$\frac{1}{2+i}$的虚部是( )
| A. | -$\frac{1}{5}$ | B. | -$\frac{1}{5}$i | C. | $\frac{1}{5}$ | D. | $\frac{1}{5}$i |
14.复数z=$\frac{-3+i}{1-i}$的共轭复数为( )
| A. | -1-i | B. | 1-i | C. | -2-i | D. | -2+i |
19.在某项调查活动中,调查部门从某单位500名职工中随机抽出100名职工,得职工年龄频率分布表.
(Ⅰ)频率分布表中的①、②位置应填什么数据?并在答题纸中补全频率分布直方图,再根据频率分布直方图估计这500名职工中年龄在[30,35)岁的人数;
(Ⅱ)在抽出的100名职工中按年龄再采用分层抽样法抽取20人参加社会公益活动,其中选取2名职工担任领队工作,记这2名职工中“年龄低于30岁”的人数为X,求X的分布列及数学期望E(X).
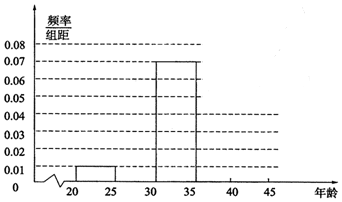
| 分组(单位:岁) | 频数 | 频率 |
| [20,25) | 5 | 0.050 |
| [25,30) | ① | 0.200 |
| [30,35) | 35 | ② |
| [35,40) | 30 | 0.300 |
| [40,45) | 10 | 0.100 |
| 合计 | 100 | 1.00 |
(Ⅱ)在抽出的100名职工中按年龄再采用分层抽样法抽取20人参加社会公益活动,其中选取2名职工担任领队工作,记这2名职工中“年龄低于30岁”的人数为X,求X的分布列及数学期望E(X).

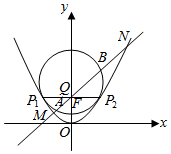 如图,抛物线C:x2=2py(p>0)的准线为y=-1,取过焦点F且平行于x轴的直线与抛物线交于不同的两点P1,P2,过P1,P2作圆心为Q的圆,使抛物线上其余点均在圆外,且∠P1QP2=90°.
如图,抛物线C:x2=2py(p>0)的准线为y=-1,取过焦点F且平行于x轴的直线与抛物线交于不同的两点P1,P2,过P1,P2作圆心为Q的圆,使抛物线上其余点均在圆外,且∠P1QP2=90°.