题目内容
德国数学家洛萨•科拉茨1937年提出了一个猜想:任给一个正整数n,如果它是偶数,就将它减半;如果它是奇数,则将它乘3再加1,不断重复这样的运算,经过有限步后,一定可以得到1.如初始正整数为6,按照上述变换规则,得到一个数列:6,3,10,5,16,8,4,2,1.现在请你研究:如果对正整数n(首项),按照上述规则实施变换后的第八项为1(第一次出现),则n的所有可能的值为 .
考点:进行简单的合情推理
专题:计算题,推理和证明
分析:可以从第八项为1出发,按照规则,逆向逐项即可求出n的所有可能的取值.
解答:
解:如果正整数n按照上述规则施行变换后的第八项为(第一次出现),
则变换中的第7项一定是2,变换中的第6项一定是4;变换中的第5项是8;变换中的第4项是16
变换中的第4项是16时,变换中的第3项是32或5,变换中的第2项是64或108,变换中的第1项是128,21或20,3
则n的所有可能的取值为3、20、21、128.
故答案为:3、20、21、128.
则变换中的第7项一定是2,变换中的第6项一定是4;变换中的第5项是8;变换中的第4项是16
变换中的第4项是16时,变换中的第3项是32或5,变换中的第2项是64或108,变换中的第1项是128,21或20,3
则n的所有可能的取值为3、20、21、128.
故答案为:3、20、21、128.
点评:本题考查的知识点是合情推理,考查新定义,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
若a+bi=
(a、b都是实数,i为虚数单位),则a+b=( )
| 25 |
| 3+4i |
| A、1 | B、-1 | C、7 | D、-7 |
若有样本容量为8的样本平均数为5,方差为2,现样本中又加入一个新数据为4,现在样本容量为9,则样本平均数和方差分别为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
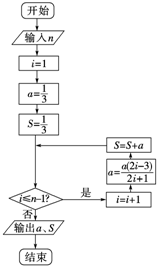 先阅读如图框图,再解答有关问题:
先阅读如图框图,再解答有关问题: 某几何体的三视图如图所示,其正视图是边长为2的正方形,侧视图和俯视图都是等腰直角三角形,则此几何体的体积是
某几何体的三视图如图所示,其正视图是边长为2的正方形,侧视图和俯视图都是等腰直角三角形,则此几何体的体积是