题目内容
10.在平面直角坐标系xOy中,曲线C的参数方程为$\left\{\begin{array}{l}{x=cosα}\\{y=1+si{n}^{2}α}\end{array}\right.$(α为参数),以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为θ=$\frac{π}{4}$,试求直线l与曲线C的交点的直角坐标.分析 将两方程化为普通方程,联立,即可求出直线l与曲线C的交点的直角坐标.
解答 解:直线l的极坐标方程为θ=$\frac{π}{4}$,直角坐标方程为y=x,曲线C的参数方程为$\left\{\begin{array}{l}{x=cosα}\\{y=1+si{n}^{2}α}\end{array}\right.$(α为参数),普通方程为y=2-x2(-1≤x≤1),
联立方程可得x2+x-2=0,∴x=1或x=-2(舍去),
∴直线l与曲线C的交点的直角坐标为(1,1).
点评 本题考查三种方程的互化,考查方程思想,正确转化是关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
15.直线m,n满足m?α,n?α,则n⊥m是n⊥α( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
2.已知方程x2+y2+4x-2y-4=0,则x2+y2的最大值是( )
| A. | $6\sqrt{5}$ | B. | $3+\sqrt{5}$ | C. | $14+6\sqrt{5}$ | D. | 14 |
19.已知数列{an}的首项a1=1,对?n∈N*,都有an+1-an≤3n,an+2-an≥4•3n成立,则a2017=( )
| A. | 32017-1 | B. | $\frac{{3}^{2017}-1}{2}$ | C. | 32017+1 | D. | $\frac{{3}^{2017}+1}{2}$ |
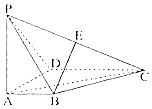 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=1,$AB=\frac{1}{2}$,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=1,$AB=\frac{1}{2}$,点E为棱PC的中点.