题目内容
8.直线l:y=kx+1与圆O:x2+y2=1相交于A,B两点,则“△OAB的面积为$\frac{1}{2}$”是“k=1”的( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
分析 根据直线和圆相交的性质,结合充分条件和必要条件的定义进行判断即可得到结论.
解答 解:若直线l:y=kx+1与圆O:x2+y2=1相交于A,B 两点,
则圆心到直线距离d=$\frac{1}{\sqrt{1{+k}^{2}}}$,|AB|=2 $\sqrt{1{-d}^{2}}$=2 $\sqrt{\frac{{k}^{2}}{1{+k}^{2}}}$,
若k=1,则|AB|=2$\sqrt{\frac{1}{2}}$=$\sqrt{2}$,d=$\frac{\sqrt{2}}{2}$,则△OAB的面积为$\frac{1}{2}$×$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=$\frac{1}{2}$成立,即必要性成立.
若△OAB的面积为$\frac{1}{2}$,则S=$\frac{1}{2}$×$\frac{1}{\sqrt{1{+k}^{2}}}$×2 $\sqrt{\frac{{k}^{2}}{1{+k}^{2}}}$=$\frac{1}{2}$×2×$\frac{|k|}{1{+k}^{2}}$=$\frac{|k|}{1{+k}^{2}}$=$\frac{1}{2}$,
即k2+1=2|k|,即k2-2|k|+1=0,
则(|k|-1)2=0,
即|k|=1,
解得k=±1,则k=1不成立,即充分性不成立.
故“△OAB的面积为$\frac{1}{2}$”是“k=1”的必要不充分条件.
故选:B.
点评 本题主要考查充分条件和必要条件的判断,利用三角形的面积公式,以及半径半弦之间的关系是解决本题的关键.

练习册系列答案
相关题目
6.在三棱锥P-ABC中,平面PAC⊥平面ABC,PA=PC=BA=BC,则直线PB与平面PAC所成的角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
16.已知一元二次不等式f(x)>0的解集为{x|x<-1或x>$\frac{1}{2}$},则f(10x)>0的解集为( )
| A. | {x|x<-1或x>lg2} | B. | {x|-1<x<lg2} | C. | {x|x>-lg2} | D. | {x|x<-lg2} |
20.设函数f(x)是定义在R上的偶函数,f'(x)为其导函数.当x>0时,f(x)+x•f′(x)>0,且f(1)=0,则不等式x•f(x)>0的解集为( )
| A. | (-∞,-1)∪(1,+∞) | B. | (-∞,-1)∪(0,1) | C. | (-1,0)∪(0,1) | D. | (-1,0)∪(1,+∞) |
18.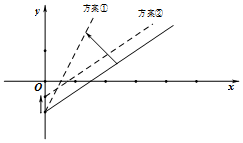 如图是某条公共汽车线路收支差额y与乘客量x的图象(实线),由于目前本线路亏损,公司有关人员提出两种扭亏为盈的方案(虚线),这两种方案分别是( )
如图是某条公共汽车线路收支差额y与乘客量x的图象(实线),由于目前本线路亏损,公司有关人员提出两种扭亏为盈的方案(虚线),这两种方案分别是( )
 如图是某条公共汽车线路收支差额y与乘客量x的图象(实线),由于目前本线路亏损,公司有关人员提出两种扭亏为盈的方案(虚线),这两种方案分别是( )
如图是某条公共汽车线路收支差额y与乘客量x的图象(实线),由于目前本线路亏损,公司有关人员提出两种扭亏为盈的方案(虚线),这两种方案分别是( )| A. | 方案①降低成本,票价不变,方案②提高票价而成本不变; | |
| B. | 方案①提高票价而成本不变,方案②降低成本,票价不变; | |
| C. | 方案①降低成本,票价提高,方案②提高票价而成本不变; | |
| D. | 方案①提高成本,票价不变,方案②降低票价且成本降低 |
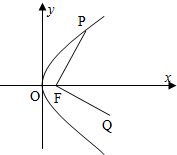 如图,点P是抛物线y2=4x上动点,F为抛物线的焦点,将向量$\overrightarrow{FP}$绕点F按顺时针方向旋转90°到$\overrightarrow{FQ}$
如图,点P是抛物线y2=4x上动点,F为抛物线的焦点,将向量$\overrightarrow{FP}$绕点F按顺时针方向旋转90°到$\overrightarrow{FQ}$