题目内容
6．在三棱锥P-ABC中，平面PAC⊥平面ABC，PA=PC=BA=BC，则直线PB与平面PAC所成的角为（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
分析 由题意画出图形，取AC中点O，连接PO，BO，可得BO⊥AC，再由面面垂直的性质可得BO⊥平面PAC，知∠BPO为直线PB与平面PAC所成的角，求解直角三角形得答案．
解答 解：如图，
设PA=PC=BA=BC=a，取AC中点O，连接PO，BO，
则BO⊥AC，
∵平面PAC⊥平面ABC，且平面PAC∩平面ABC=AC，
∴BO⊥平面PAC，则∠BPO为直线PB与平面PAC所成的角，
∵PA=PC=BA=BC，AC=AC，
∴△PAC≌△BAC，则PO=OB，
∴∠BPO=45°，
故选：B．
点评 本题考查直线与平面所称的角，考查空间想象能力和思维能力，是中档题．
练习册系列答案
相关题目
16．
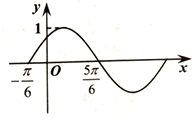函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则关于f（x）的说法正确的是（ ）
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则关于f（x）的说法正确的是（ ）| A． | 对称轴方程是x=$\frac{π}{3}$+2kπ（k∈Z） | B． | φ=-$\frac{π}{6}$ | ||
| C． | 最小正周期为π | D． | 在区间（$\frac{π}{2}$，$\frac{7π}{6}$）上单调递减 |
17．如图，在△ABC中，若AB=5，AC=7，∠B=60°，则BC等于（ ）
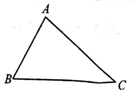
| A． | $5\sqrt{3}$ | B． | $6\sqrt{2}$ | C． | 8 | D． | $5\sqrt{2}$ |
1．过点A（2，1），且与直线x+2y-1=0垂直的直线方程为（ ）
| A． | x+2y-4=0 | B． | x-2y=0 | C． | 2x-y-3=0 | D． | 2x+y-5=0 |
3．过点P（0，1），且与点A（3，3）和B（5，-1）的距离相等的直线方程是（ ）
| A． | y=1 | B． | 2x+y-1=0 | ||
| C． | y=1或2x+y-1=0 | D． | 2x+y-1=0或2x+y+1=0 |
8．直线l：y=kx+1与圆O：x2+y2=1相交于A，B两点，则“△OAB的面积为$\frac{1}{2}$”是“k=1”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分又不必要条件 |