题目内容
3.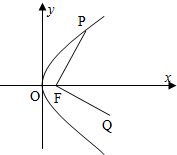 如图,点P是抛物线y2=4x上动点,F为抛物线的焦点,将向量$\overrightarrow{FP}$绕点F按顺时针方向旋转90°到$\overrightarrow{FQ}$
如图,点P是抛物线y2=4x上动点,F为抛物线的焦点,将向量$\overrightarrow{FP}$绕点F按顺时针方向旋转90°到$\overrightarrow{FQ}$(Ⅰ)求Q点的轨迹C的普通方程;
(Ⅱ)过F倾斜角等于$\frac{π}{4}$的直线l与曲线C交于A、B两点,求|FA|+|FB|的值.
分析 (I)设Q(x,y),P(a,b),则$\frac{b}{a-1}•\frac{y}{x-1}$=-1,(a-1)2+b2=(x-1)2+y2,b=x-1,a=-(y-1),即可求Q点的轨迹C的普通方程;
(Ⅱ)设A,B对应的参数分别为t1,t2,联立方程求出结合|FA|+|FB|=|t1|+|t2|,进行计算即可.
解答 解:(I)设Q(x,y),P(a,b),
则$\frac{b}{a-1}•\frac{y}{x-1}$=-1,(a-1)2+b2=(x-1)2+y2,
∴b=x-1,a=-(y-1),
∵b2=4a,
∴(x-1)2=-4(y-1)
(II)过F倾斜角等于$\frac{π}{4}$的直线l的参数方程为$\left\{\begin{array}{l}{x=1+\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$,
设A,B对应的参数分别为t1,t2,把直线的参数方程代入曲线方程得t2+4$\sqrt{2}$t-8=0,
则t1+t2=-4$\sqrt{2}$,t1t2=-8,
∴t1>0,t2<0,
则|FA|+|FB|=|t1|+|t2|=$\sqrt{32+32}$=8.
点评 本题主要考查轨迹方程,考查直线参数方程的运用,属于中档题.

练习册系列答案
相关题目
1.过点A(2,1),且与直线x+2y-1=0垂直的直线方程为( )
| A. | x+2y-4=0 | B. | x-2y=0 | C. | 2x-y-3=0 | D. | 2x+y-5=0 |
18.函数f(x)=ax2+bx+2a-b是定义在[a-1,2a]上的偶函数,则a+b=( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | 0 | D. | 1 |
8.直线l:y=kx+1与圆O:x2+y2=1相交于A,B两点,则“△OAB的面积为$\frac{1}{2}$”是“k=1”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |