题目内容
6.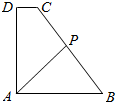 如图,直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=AB=4,CD=1,动点P在边BC上,且满足$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AD}$(m,n均为正实数),则$\frac{1}{m}+\frac{1}{n}$的最小值为$\frac{7+4\sqrt{3}}{4}$.
如图,直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=AB=4,CD=1,动点P在边BC上,且满足$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AD}$(m,n均为正实数),则$\frac{1}{m}+\frac{1}{n}$的最小值为$\frac{7+4\sqrt{3}}{4}$.
分析 假设$\overrightarrow{BP}$=λ$\overrightarrow{BC}$,用$\overrightarrow{AB},\overrightarrow{AD}$表示出$\overrightarrow{AP}$,使用平面向量的基本定理得出m,n与λ的关系,得到$\frac{1}{m}+\frac{1}{n}$关于λ的函数,求出函数的最值.
解答 解:$\overrightarrow{AC}=\overrightarrow{AD}+\overrightarrow{DC}$=$\frac{1}{4}\overrightarrow{AB}+\overrightarrow{AD}$,$\overrightarrow{BC}$=$\overrightarrow{AC}-\overrightarrow{AB}$=-$\frac{3}{4}\overrightarrow{AB}$+$\overrightarrow{AD}$,
设$\overrightarrow{BP}$=λ$\overrightarrow{BC}$=-$\frac{3λ}{4}$$\overrightarrow{AB}$+λ$\overrightarrow{AD}$(0≤λ≤1),
则$\overrightarrow{AP}$=$\overrightarrow{AB}+\overrightarrow{BP}$=(1-$\frac{3λ}{4}$)$\overrightarrow{AB}$+λ$\overrightarrow{AD}$.
∵$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AD}$,∴m=1-$\frac{3λ}{4}$,n=λ.
∴$\frac{1}{m}+\frac{1}{n}$=$\frac{4}{4-3λ}+\frac{1}{λ}$=$\frac{λ+4}{-3{λ}^{2}+4λ}$=$\frac{1}{28-(3(λ+4)+\frac{64}{λ+4})}$≥$\frac{1}{28-2\sqrt{3×64}}$=$\frac{7+4\sqrt{3}}{4}$.
当且仅当3(λ+4)=$\frac{64}{λ+4}$即(λ+4)2=$\frac{64}{3}$时取等号.
故答案为:$\frac{7+4\sqrt{3}}{4}$.
点评 本题考查了平面向量的基本定理,向量的线性运算的几何意义,基本不等式,属于中档题.

| A. | (-12,3] | B. | (-12,3) | C. | (-12,4] | D. | (-12,4) |
| A. | 1 | B. | $\frac{\sqrt{5}}{5}$ | C. | 2 | D. | $\sqrt{5}$ |
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{8}$ | D. | $\frac{3π}{4}$ |
 如图,一船自西向东匀速航行,上午10时到达一座灯塔P的南偏西75°距灯塔60海里的M处,下午2时到达这座灯塔的东偏南45°的N处,则该船航行的速度为$\frac{15\sqrt{6}}{2}$海里/小时.
如图,一船自西向东匀速航行,上午10时到达一座灯塔P的南偏西75°距灯塔60海里的M处,下午2时到达这座灯塔的东偏南45°的N处,则该船航行的速度为$\frac{15\sqrt{6}}{2}$海里/小时.