题目内容
18. 如图,一船自西向东匀速航行,上午10时到达一座灯塔P的南偏西75°距灯塔60海里的M处,下午2时到达这座灯塔的东偏南45°的N处,则该船航行的速度为$\frac{15\sqrt{6}}{2}$海里/小时.
如图,一船自西向东匀速航行,上午10时到达一座灯塔P的南偏西75°距灯塔60海里的M处,下午2时到达这座灯塔的东偏南45°的N处,则该船航行的速度为$\frac{15\sqrt{6}}{2}$海里/小时.
分析 根据正弦定理解出MN即可求得速度.
解答 解:N=45°,∠MPN=75°+45°=120°,
在△PMN中,由正弦定理得$\frac{PN}{sinN}=\frac{MN}{sin∠MPN}$,即$\frac{60}{sin45°}=\frac{MN}{sin120°}$,
解得MN=$\frac{60sin120°}{sin45°}$=30$\sqrt{6}$(海里).
∵轮船航行时间为4小时,
∴轮船的速度为$\frac{30\sqrt{6}}{4}$=$\frac{15\sqrt{6}}{2}$海里/小时.
故答案为$\frac{15\sqrt{6}}{2}$.
点评 本题考查了正弦定理,解三角形的应用,属于基础题.

练习册系列答案
相关题目
3.已知a=($\frac{1}{2}$)${\;}^{\frac{1}{3}}}$,b=($\frac{1}{3}$)${\;}^{-\frac{1}{2}}}$,c=log2$\frac{1}{3}$,则a,b,c的大小关系是( )
| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | b<a<c |
7.某同学用“五点法”画函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入的部分数据如下表:
(Ⅰ)求x2的值及函数f(x)的解析式;
(Ⅱ)请说明把函数g(x)=sinx的图象上所有的点经过怎样的变换可以得到函数f(x)的图象.
| x | x1 | $\frac{π}{12}$ | x2 | $\frac{7π}{12}$ | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin(ωx+φ)+B | 1 | 4 | 1 | -2 | 1 |
(Ⅱ)请说明把函数g(x)=sinx的图象上所有的点经过怎样的变换可以得到函数f(x)的图象.
8.设α∈(0,$\frac{π}{2}$),sinα=$\frac{\sqrt{6}}{3}$,则tanα等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
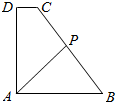 如图,直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=AB=4,CD=1,动点P在边BC上,且满足$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AD}$(m,n均为正实数),则$\frac{1}{m}+\frac{1}{n}$的最小值为$\frac{7+4\sqrt{3}}{4}$.
如图,直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=AB=4,CD=1,动点P在边BC上,且满足$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AD}$(m,n均为正实数),则$\frac{1}{m}+\frac{1}{n}$的最小值为$\frac{7+4\sqrt{3}}{4}$.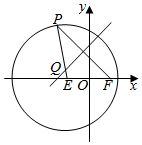 如图,已知圆E:(x+$\sqrt{3}$)2+y2=16,点F($\sqrt{3}$,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
如图,已知圆E:(x+$\sqrt{3}$)2+y2=16,点F($\sqrt{3}$,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.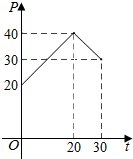 据市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t (t∈N)(天)的关系如图所示.
据市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t (t∈N)(天)的关系如图所示.