题目内容
15.若函数f(x)=sinx+cosx,则f′($\frac{π}{2}$)的值为( )| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
分析 根据基本导数公式求导即可.
解答 解:f′(x)=cosx-sinx,
∴f′($\frac{π}{2}$)=cos$\frac{π}{2}$-sin$\frac{π}{2}$,
故选D
点评 本题考查了导数的运算法则和导数值的求法,属于基础题.

练习册系列答案
相关题目
7.函数y=x2+x+1的极小值是( )
| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{7}{4}$ | D. | 不存在 |
3.已知a=($\frac{1}{2}$)${\;}^{\frac{1}{3}}}$,b=($\frac{1}{3}$)${\;}^{-\frac{1}{2}}}$,c=log2$\frac{1}{3}$,则a,b,c的大小关系是( )
| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | b<a<c |
7.某同学用“五点法”画函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入的部分数据如下表:
(Ⅰ)求x2的值及函数f(x)的解析式;
(Ⅱ)请说明把函数g(x)=sinx的图象上所有的点经过怎样的变换可以得到函数f(x)的图象.
| x | x1 | $\frac{π}{12}$ | x2 | $\frac{7π}{12}$ | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin(ωx+φ)+B | 1 | 4 | 1 | -2 | 1 |
(Ⅱ)请说明把函数g(x)=sinx的图象上所有的点经过怎样的变换可以得到函数f(x)的图象.
5.已知具有线性相关关系的两个量x,y之间的一组数据如表:
且回归直线方程是$\widehat{y}$=0.95x+2.6,则m的值为( )
| x | 0 | 1 | 2 | 3 | 4 |
| y | 2.2 | 4.3 | 4.5 | m | 6.7 |
| A. | 4.5 | B. | 4.6 | C. | 4.7 | D. | 4.8 |
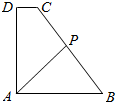 如图,直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=AB=4,CD=1,动点P在边BC上,且满足$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AD}$(m,n均为正实数),则$\frac{1}{m}+\frac{1}{n}$的最小值为$\frac{7+4\sqrt{3}}{4}$.
如图,直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=AB=4,CD=1,动点P在边BC上,且满足$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AD}$(m,n均为正实数),则$\frac{1}{m}+\frac{1}{n}$的最小值为$\frac{7+4\sqrt{3}}{4}$.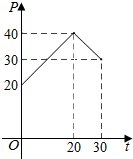 据市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t (t∈N)(天)的关系如图所示.
据市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t (t∈N)(天)的关系如图所示.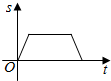 如图是王老师锻炼时所走的离家距离(S)与行走时间(t)之间的函数关系图,若用黑点表示王老师家的位置,则王老师行走的路线可能是( )
如图是王老师锻炼时所走的离家距离(S)与行走时间(t)之间的函数关系图,若用黑点表示王老师家的位置,则王老师行走的路线可能是( )